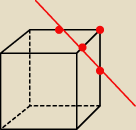
/ HELPP: Sześcian o długości krawędzi a przecinamy płaszczyzną przechodzącą przez środki każdej krawędzi wychodzącej z jednego wierzchołka. Objętość odciętego ostrosłupa jest równa?

	1
A		a/div>
	8

	1
B		a3
	12

	1
C		a3
	16

	1
D		a3
	48

Wiem że V całęgo sześcianu to a³ ale nie wiem jak się wziąć za ten odcięty kawałek

ICSP: Podstawa : trójkąt prostokątny o bokach: a/2 , a/2 , a√2/2 Wysokość : a/2

	1		1		1		a		a		a
V =		Pp * H =		*		*		*		*		= ...
	3		3		2		2		2		2

oli: tu masz lepszy rysunek https://matematykaszkolna.pl/forum/264266.html

wredulus_pospolitus: odcięty jest ostrosłup który można ustawić tak, że:

	a
1) podstawą jest trójkąt prostokątny (patrz górna ściana sześcianu) o przyprostokątnych
	2

	a
2) wysokość jest będzie także równa
	2

3) Więc jego objętość będzie równa

HELPP: Dziękuje