sześcian
mia: sześcian o krawędzi 4 przecięto płaszczyzną przechodzącą przez środki krawędzi wychodzących z
jednego wierzchołka. oblicz pola pow całkowitych i objętości otrzymanych w ten sposób
wielościanów.
proszę o pomoc, kompletnie nie wiem jak się do tego zabrać
5 lis 17:33
mia: jakieś wskazówki

5 lis 17:53
mia: proszę o pomoc
5 lis 18:03
mia: ?
5 lis 18:23
mia: pomóżcie
5 lis 18:36
dero2005:
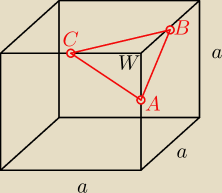
5 lis 18:44
dero2005:
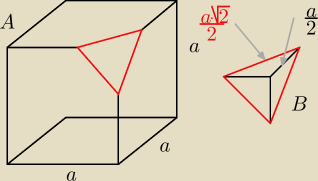
objętość bryły B
| | | | a | | 1 | | a3 | |
VB = |
| * |
| * |
| = |
| |
| | 2 | | 2 | | 3 | | 48 | |
Pole bryły B
| | | | (a2)2 | | 6+√3 | |
Pc = |
| *3 + |
| *√3 = a2( |
| ) |
| | 2 | | 4 | | 16 | |
5 lis 19:00
dero2005:
objętość bryły A
| | a3 | | 47a3 | |
VA = a3 − |
| = |
| |
| | 48 | | 48 | |
pole powierzchni bryły A
| | | | (a2)2 | |
Pc = 6a2 − |
| *3 + |
| *√3 = |
| | 2 | | 4 | |
dokończ

5 lis 19:05
dero2005:
oczywiście nie uniknąłem pomyłki, zaraz poprawię
5 lis 19:07
dero2005:
oznaczmy odcinek czerwony bryły B literą c
| | b2 | | c2√3 | |
Pole bryły B = |
| *3 + |
| = |
| | 2 | | 4 | |
Objętość bryły A
pole bryły A
| | b2 | | c2√3 | |
PA = 6a2 − |
| *3} + |
| = |
| | 2 | | 4 | |
po podstawieniu jak wyżej dokończ
5 lis 19:15


 objętość bryły B
objętość bryły B
