 Na kuli o promieniu R=4cm opisano stożęk
Walczę z tym zadaniem: 835
Wiem, że jest do niego rozwiązanie jednak próbuje wyznaczyć pochodną po H zamiast po R i za
żadne skarby nie chce mi wyjść wynik.
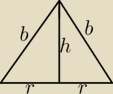
b=√r2+h2
Na kuli o promieniu R=4cm opisano stożęk
Walczę z tym zadaniem: 835
Wiem, że jest do niego rozwiązanie jednak próbuje wyznaczyć pochodną po H zamiast po R i za
żadne skarby nie chce mi wyjść wynik.
b=√r2+h2
| 2rh | ||
p= | ||
| 2 |
| abc | ||
p= | ||
| 4R |
| 2rh | 2r*(r2+h2) | ||
= | |||
| 2 | 4*4 |
| 2r3+2rh2 | ||
rh= | /*16 | |
| 16 |
| 1 | ||
V= | π r2 h | |
| 3 |
| 1 | ||
V= | π (8h−h2) h | |
| 3 |
| 1 | ||
V= | π (8h2−h3) | |
| 3 |
| 1 | ||
P'(h)= | π * (16h−3h2) | |
| 3 |
| 16 | ||
jest maksimum lokalne. Co robię źle bo odpowiedz powinna być 16! Dodatkowo nie wiem | ||
| 3 |
| a*b*c | ||
P= | , R− promień okręgu opisanego na Δ, | |
| 4R |
| a+b+c | ||
PΔ= | *R, gzie R=4 | |
| 2 |
| b+b+2r | ||
PΔ= | *4 | |
| 2 |