Równanie ogólne prostej. Kę: Punkty A(2,−3) i B(5,1) są wierzchołkami trójkąta ABC. Bok BC zawiera się w prostej k: x+2y−7=0, zaś środkowa AM zawiera się w prostej m: 5x−y−13=0. Wyznacz równanie ogólne prostej, w której zawiera się wysokość trójkąta poprowadzona z wierzchołka C. Wyszło mi 3x−4y+9=0, a powinno 3x−4y−15=0. Może ktoś mi powiedzieć gdzie mam błąd, bo nie mogę znaleźć? No chyba, że odpowiedź w zbiorze jest zła.

Kę: Prosta AB wyszła mi: 4x+3y−23=0 ; M=(3,2) ; C(1,3)

Kę: Pomoże mi ktoś?

ABC: Prosta AB 4x−3y−17=0 dalej nie patrzyłem

Kę: Dziękuję! Walnąłem się w liczeniu prostej AB i dlatego nie wyszło

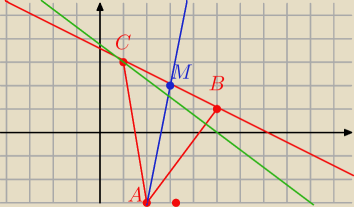
janek191: 2y = − x + 7 y = −0,5 x + 3,5 y = 5 x − 13 więc −0,5 x + 3,5 = 5 x − 13 / * 2 − x + 7 = 10 x − 26 11 x = 33 x = 3 y = 2 M = ( 3, 2) ========= B = ( 5, 1) → BM = [− 2, 1 ] C = ( 3 − 2, 2 + 1) = ( 1, 3) ======================== Prosta AB

	4
a =
	3

Prosta CD

	3
y = −		x + b
	4

	3
3 = −		*1 + b
	4

	3
b = 3
	4

	3		15
y = −		x +		/ * 4
	4		4

4 y = − 3 x + 15 3 x + 4 y − 15 = 0 ===============

Kę: Mam inne rozwiązanie, więc fajnie zobaczyć inne

Kę: https://matematykaszkolna.pl/forum/99259.html jest tutaj rozwiązany jeden przypadek. Czy może jakaś osóbka wie, jak pooznaczać trójkąt w drugim przypadku?