trójat
lizinczyk: W trójkącie ABC ,gdzie AB=5, wybrano punkty E i F tak ze BE = 1, EF = 3 , CF = 2. AE oraz AF
przecinają okkrąg opisany na trójkacie ABC odpowiednio w punktach G oraz H. GH oraz BC są
równoległe.
Zakładając że AC=a*√a/c, oblicz a+c.
23 lut 11:15
6latek:
23 lut 17:52
6latek: Podbijam chociaz to nie moje zadanie
23 lut 18:15
lizinczyk: Co oznacza podbijanie?
23 lut 20:21
a47: (1.1) nadawać ruch lub używać siły, uderzając od spodu
(1.2) zwyciężać i brać pod swoje panowanie
(1.3) przen. zdobywać czyjąś życzliwość, miłość lub sympatię
(1.4) mocować coś do czegoś od spodu
(1.5) oferować wyższą stawkę w licytacji
23 lut 20:25
Mila:
To znaczy, że chciałby aby ktoś rozwiązał. Zadanie pojawia się na początku strony ( przez
jakiś czas).
Ja mam pytanie, czy dokładnie przepisałeś treść zadania.
Jeżeli BE, EF,CF są odcinkami BC , to znaczy , że a=1+3+2, c=5 i nie ma co liczyć.
23 lut 20:27
24 lut 01:01
lizinczyk : A jak obliczyc AC?
24 lut 13:21
lizinczyk : Nie wiem skąd wiełaś ze c=5?
24 lut 13:22
lizinczyk: podbijam
25 lut 16:56
lizinczyk: 6latek jakos chyba to podbijanie nie działa
25 lut 18:31
as:
Skąd masz ten wzór? Jest jakaś wskazówka do zadania?
AC=a*√a/c,
25 lut 19:06
lizinczyk: To nie wzór porostu założenie tylko. Wynik AC ma być tej postaci. I muszę potem obliczyć a+c.
25 lut 20:04
an: Czy a,b,c to są boki trójkąta ABC, jezeli tak to >> Zakładając że AC=a*√a/c, oblicz a+c.<<
to nie ma praktycznie czego liczyć, ale nie pasuje to do początku zadania. odpowiedź
zbliżona do b≈7,92
25 lut 20:07
lizinczyk: a, b, c to nie są boki trójkąta żadnego
25 lut 20:13
lizinczyk: Równie dobrze mogłoby być x√x/y i obliczyć x+y
25 lut 20:16
Mila:
Coś tam wymyśliłam, jeszcze sprawdzę poprawność. Jutro wieczorem się odezwę.

Zauważ, że ten czworokąt BGHC jest trapezem równoramiennym.
26 lut 00:12
lizinczyk: ok poczekam
26 lut 14:38
lizinczyk: Czemu BGHC jest trapezem równoramiennym?
26 lut 19:02
an: Czworokąt BGHC jest trapezem równoramiennym gdyż posiada dwie podstawy rórnoległe do siebie
i jest wpisany w okrąg to jest oczywista oczywistość
26 lut 20:02
Mila:
Trapez wpisany w okrąg jest równoramienny.
https://www.matmana6.pl/czworokaty-wpisane-w-okrag
an, obliczyłaś długość AC. A może masz odpowiedź ze zbioru?
O ile to zadanie jest z jakiegoś zbioru.
Ja obliczyłam, ale źle napisałam jedną proporcję ( coś zgubiłam i pięknie wyszło)
i znowu muszę pomyśleć.
26 lut 21:17
an: Niestety nie obliczyłem wyszło z rysunku jest nieco ponad 7,9, wydaje mi się, że to ma coś
wspólnego z geometrią wykreślną, ale to było strasznie dawno.
26 lut 21:45
Mila:

Dziękuję.
26 lut 22:17
miki:
20 mar 05:45
miki: Czy wyszło 62,5 ?
20 mar 15:25
miki: 
?
21 mar 21:38
x:
Co obliczyłeś Miki?
21 mar 22:56
miki: Bok AC, kto policzyl go jeszcze?
22 mar 19:23
miki: Nikt więcej nie policzyl czy co
23 mar 20:19
Mila:
Nie może mieć takiej długości, bo boki Δ: 5+6<62.5
Coś mi tam brakuje w treści tego zadania, skąd masz to zadanie?
23 mar 21:06
iteRacj@: Milu to 62,5 to chyba nie jest długość boku AC. To jest suma liczb a+c, przy założeniu, że
obliczoną długość boku AC przedstawimy w postaci a*√a/c.
23 mar 21:20
Mila:
Masz jakieś konstruktywne rachunki?
23 mar 21:59
iteRacj@: Długości AC nie udało mi się policzyć : ((
| | a | |
Natomiast suma a+c równa około 62 jest możliwa. Wtedy |AC|=a*√ |
| . |
| | 62−a | |
| | a | |
Dla np. a=16 i a*√ |
| ≈9,43, nierównośc trojkąta jest spełniona. |
| | 62−a | |
23 mar 22:35
iteRacj@: Liczę, że ktoś wpisze rozwiązanie, to się dowiem, co i jak tu trzeba policzyć, bez zgadywania.
23 mar 22:41
Mila:
hm?
23 mar 22:43
a7: no ja nie znalazłam nic w necie poza rysunkiem
23 mar 22:48
23 mar 22:49
23 mar 23:04
miki: To w końcu jaka jest odpowiedź?
24 mar 00:34
a7: a jak Tobie wyszło i jakim sposobem, bo na razie bardziej konkretnej odpowiedzi tutaj nie ma
24 mar 00:58
miki: nie sorry
√62,5
24 mar 01:15
a7: ale jak wyszedł ten wynik to sprawdzimy, i w razie czego można go będzie skorygować lub Twoje
spostrzeżenia umożliwią potwierdzenia prawidłowości rozwiązania lub być może zainspirują do
prawidłowego rozwiązania zadania

24 mar 01:25
miki: a) BGHC jest równoramienny
b) ABF i HFC są podobne wiec 4HC=5FH
c) ACF i HFB są podobne FH=2⋅BH/AC
d) BEA i GCE są podobne oraz BGHC jest równoramienny więc BH=25/AE
e) z b),c),d) HC=125/(2⋅AC⋅AE)
f) BEG i AEC są podobne oraz BGHC jest równoramienny więc HC=AC/AE
z e) i f) AC
24 mar 08:09
Mila:
|AC|=b
b=5
√52
5+2=7
24 mar 18:46
Mila:
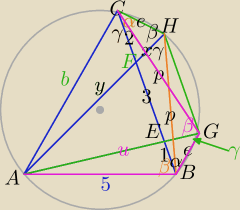
1) W czworokącie ABHC:
|CH|=e , |BH|=p
| x | | 2 | | 2p | | 5 | | 2p | | 5p | |
| = |
| ⇔x= |
| ⇔e= |
| * |
| = |
| ⇔ |
| p | | b | | b | | 4 | | b | | 2b | |
=========
2) W czworokącie ABGC:
3) Podstawiając do (*) za p
i porównanie:
b=5*
√52
a=5, c=2
a+c=5+2=7
==========
24 mar 20:42
a7: mistrzostwo

24 mar 21:46
Mila:
Nie ma błędu?
Liczyłam z tw. cosinusów, ale takie obliczenia , że ciągle się mylę.
Jak zgodzą się rachunki to wpiszę.
24 mar 22:00
a7: | | e | | 5 | |
szczerze mówiąc to głupio , ale nie wiem już na początku dlaczego |
| = |
| potem nie |
| | x | | 4 | |
wiem czemu x/p=2/b itd.,
24 mar 22:05
Mila:
W podanych czworokątach masz po dwie pary trójkątów podobnych.
Patrząc na kąty układasz proporcje.
Będą kłopoty to napiszę z oznaczeniami .
24 mar 22:23
Mila:
Miki wypisał trójkąty podobne.
24 mar 22:25
a7: no właśnie coś nie widzę tych trójkątów podobnych, ale miki chyba zauważył bo też z tego
korzystał

24 mar 22:29
Mila:
Jutro Ci wypiszę dokładnie, teraz katar mnie dopadł więc chyba pójdę spać

Dobranoc

24 mar 22:41
a7: Dobranoc

24 mar 22:42
Mila:
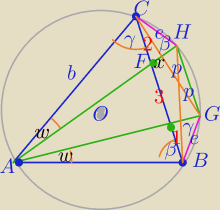
BGHC− trapez równoramienny
|CG|=|BH|=p, |FH|=e
| | e | | 5 | |
1) WΔCFH i ΔAFB: |
| = |
| , |
| | x | | 4 | |
| | x | | 2 | |
2) W ΔFHB i ΔCFA: |
| = |
| |
| | p | | b | |
======
| | p | | 5 | |
3) W ΔCEG i ΔAEB: |
| = |
| , |
| | 5 | | u | |
| | e | | b | |
4) W ΔGEB i ΔAEC: |
| = |
| , |
| | 1 | | u | |
5)
===========
6) porównanie p:
|AC|=5
√52
=========
25 mar 15:45
25 mar 17:26
a7: @Mila BARDZO DZIĘKUJĘ

za bardziej szczegółowe opisanie tych podobnych trójkątów wprawdzie ja
ich dalej nie widzę (tj. nie widzę tych kątów identycznych), ale to pewnie zadanie z jakiejś
olimpiady, konkursu itp. więc się obejdę
26 mar 23:57
Mila:
a7 Patrz na kąty wpisane oparte na tym samym łuku.
27 mar 19:21
 Zauważ, że ten czworokąt BGHC jest trapezem równoramiennym.
Zauważ, że ten czworokąt BGHC jest trapezem równoramiennym.
 Dziękuję.
Dziękuję.
 ?
?


 1) W czworokącie ABHC:
|CH|=e , |BH|=p
1) W czworokącie ABHC:
|CH|=e , |BH|=p


 Dobranoc
Dobranoc 

 BGHC− trapez równoramienny
|CG|=|BH|=p, |FH|=e
BGHC− trapez równoramienny
|CG|=|BH|=p, |FH|=e
 za bardziej szczegółowe opisanie tych podobnych trójkątów wprawdzie ja
ich dalej nie widzę (tj. nie widzę tych kątów identycznych), ale to pewnie zadanie z jakiejś
olimpiady, konkursu itp. więc się obejdę
za bardziej szczegółowe opisanie tych podobnych trójkątów wprawdzie ja
ich dalej nie widzę (tj. nie widzę tych kątów identycznych), ale to pewnie zadanie z jakiejś
olimpiady, konkursu itp. więc się obejdę