pieciokat lizinczyk: ABCDE jest pięciokatem wpiasny w okrąg. Wiadomo, że AC= 2, AD= 3, BD=5, BE =1 oraz CD/DE = 10/3 , BC/CE = a/b (gdzie a i b są względnie pierwsze). Wyznacz różnicę a−b?

miki: Niech CD=10x, DE=3x, CE=y, BC=z. Które tutaj są równe katy?

an: AD=3; DB=5; BE=1 czy tak jest w zadaniu przy kolejnym oznaczeniu wierzchołków nie jest to możliwe

miki: Czemu AD=3; DB=5; BE=1 nie jest to możliwe?

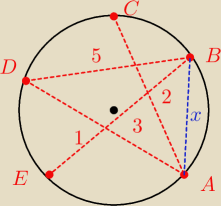
wredulus_pospolitus: Ponieważ |AB| < |AC| ... więc |AD| + |AB| < |AD| + |AC| = 2 + 3 = 5 = |BD| więc jakim cudem możesz mieć ΔABD

miki: Czemu oznaczyłes AB=x?

miki: Chyba ten rysunek jest błedny 1=EB>DB=5

wredulus_pospolitus: Oczywiście, ze rysunek jest 'błędny'. Chociażby dlatego, że ABCDE na rysunku jest praktycznie pięciokątem foremnym ... ale rysunek jest tylko POGLĄDOWY Istotne jest zrozumieniem dlaczego |AB| = x < 2 = |AC| (a tak niestety MUSI być przy takich danych), a to powoduje, że nie istnieje coś takiego jak ΔABD. Tak więc − sprawdź treść zadania