mam problem z rozwiązaniem zadania na poziomie kl7sp ika: Sześcian rozcięto płaszczyzną przechodzącą przez przekątną jednej z jego ścian na dwie części iw ten sposób, że utworzony przekrój jest trójkątem równobocznym o polu 6 √3 Ile wynosi.objętość mniejszej (co do objętości) z tych części

wredulus_pospolitus: skoro jest to trójkąt równoboczny to znaczy że przekrój idzie przez przekątne kolejnych dwóch ścian Masz pole przekroju ... to licz ile wynosi długość krawędzi sześcianu ... liczysz objętość ostrosłupa trójkątnego prostokątnego o przyprostokątnych równych 'a' i wysokości 'a'

ika: Nie rozumiem, kilka razy wyszedł mi wynik V=4√6jm3, wiem ,że błedny. Z moich wyliczeń a=2√6, h=3√2 i dalej błądzę. Proszę o wskazówki

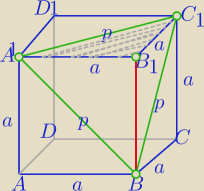
Mila: 1)Długość boku przekroju (ΔA₁BC₁)

	p2√3
		=6√3 /:√3
	4

p²=4*6=24 2) Długość krawędzi sześcianu: w ΔBAA₁ p²=a²+a² 24=2a² a²=12 a=√12=2√3 3) Objętość ostrosłupa (A₁C₁BB1) − to jest naroże sześcianu, krawędzie wychodzące z wierzchołka B₁ są do siebie prostopadłe. Jako podstawę przyjmijmy ΔA₁B¹C₁, H=BB₁=a

	1		1
V=		*(		*a*a)*a
	3		2

	1		1		1
V=		a3=		*a2*a=		*12*2√3
	6		6		6

dokończ

iteRacj@: @Milu Jak przeprowadzic dowód w tym zadaniu? 386280

ika: Bardzo dziękuję, teraz widzę ten przekrój i trójkąt równoboczny, którego bok jest przeciwprostokątną trójkąta AA'B i z tego należało wyliczyć a no i oczywiście dalej... V=4√3 Serdecznie pozdrawiam

Mila: ika rysunek zawsze pomaga Iteracjo, już patrzę, ale będę około 20. Muszę mieć teraz czas na domowe zajęcie.