trójkat
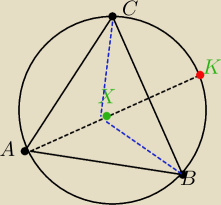
Dada: W trokacie ABC dwusieczna kata BAC przecina okrag na nim opisany w punkcie K. Wykaż że
BX + CX ≥ AK
gdzie X środek odcinka AK.
16 lut 00:02
Wish you were here:
Jedynie co przychodzi mi do glowy to taka nierownosc
BX+CX≥BC
16 lut 08:25
Wish you were here: Nie ja jestem autorem tego zadania ale interesuje mnie jego rozwiazanie
16 lut 09:25
Jula: Czy to zadanie z liceum?
16 lut 16:22
Wish you were here: Mysle ze tak .
16 lut 16:25
Mila:
wg tego rysunku: (08:25) ( szczególny przypadek)
|BX|+|CX|=2R=|AK|
Trzeba rozważyć sytuację gdy dwusieczna kąta A nie przechodzi przez środek okręgu.
17 lut 18:37
iteRacj@:
I właśnie to mi się nie udało 👎...
17 lut 18:48
ABC:
Iteracja próbowałaś coś wycisnąć z twierdzenia o trójliściu?
17 lut 18:54
iteRacj@:
Próbowałam. Wyszło kilka pięknych dowodów, niestety nie tej tezy....
17 lut 18:58
Dada: na pewno nie bedzie to z jakiegos twierdzenia o trójlisciu bo go nie mielismy
17 lut 21:02
Mila:
Z której klasy to zadanie?
17 lut 21:20
Dada: 3cia
17 lut 21:25
23 lut 21:32
iteRacj@:
Dzięki.
Ciekawe skąd to zadanie, może jednak nie z trzeciej gimnazjum.
23 lut 21:50
ABC:
może i nie
23 lut 21:52
Eta:
ABC ...co tak ciągle "skaczesz" ?
23 lut 21:59
ABC:
Eta bo dojrzałość to gorzkie rozczarowanie, na które jedynym lekarstwem jest skakanie
23 lut 22:01
krecik:
6 cze 18:48
https://www.matematyka.pl/viewtopic.php?f=110&t=439249