Geometria analityczna. cardi bardi : Na prostej k o równaniu 4x−y−2=0 wyznacz punkt C tak, aby pole trójkąta ABC, gdzie A=(5, −1), B=(1,3) było równe 8.

jc: https://matematykaszkolna.pl/forum/384178.html

cardi bardi : Wyznaczyłem punkt C jako (x_c, 4x_c −2), po czym podstawiłem do wzoru na pole trójkąta kiedy

	1		1
mamy współrzędne 3 boków (jest w tablicach). Wyszło mi xc=		lub xc= 3		. Co
	2		6

robię źle?

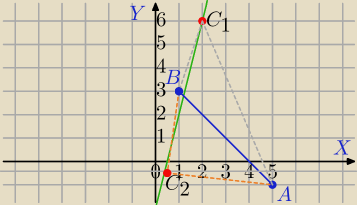
Mila: k: 4x−y−2=0⇔y=4x−2 A=(5, −1), B=(1,3) AB^→=[−4,4] C=(x,4x−2) AC^→=[x−5,4x−2+1]=[x−5,4x−1]

	1
PΔABC=		*|W|
	2

x−5 4x−1 −4 4 W=4*(x−5)+4*(4x−1)=4x−20+16x−4

1
	*|20x−24|=8
2

|10x−12|=8 /: 2 |5x−6|=4 5x−6=4 lub 5x−6=−4

	2
x=2 lub x=
	5

	2		2
C1=(2, 6) lub C2=(		,−		)
	5		5

Eta: Wiedziałam ,że Mila nie wytrzyma i poda gotowca !

cardi bardi : Dziękuję <3 Mnie również wyszło, po prostu błąd rachunkowy.

Eta: I tak trzymaj wniosek : zawsze sprawdzaj po dwa razy obliczenia