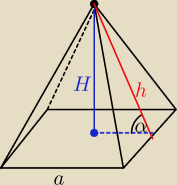
ostrosłup matura19: W ostrosłupie prawidłowym czworokątnym pole ściany bocznej jest równe 12 a cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy jest równy 1/3 Oblicz objętość ostrosłupa

Maciess: o maturka próbna z nowej ery

Maciess:

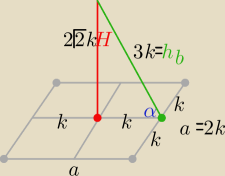
Eta: ............ P_s=k*3k ⇒ 3k²=12 ⇒ k=2>0

	1
V=		*4k2*2√2k
	3

	64√2
V=		j3
	3

≈≈≈≈≈≈≈≈≈≈≈

Maciess:

	12a		12a		3a
cosα=		⇒ h=		=
	h		cosα		2

P_ściany=12

ah		a*3a/2		3a2
	=		=
2		2		4

3a2
	=12
4

a²=16 a>0 ⇒ a=4 h=6

	a
H2=h2−(		)2
	2

H²=36−4=32 H=4√2

	1		1		64√2
V=a2*H*		=16*4√2*		=
	3		3		3

Maciess: Dłuzej pisałem, ale przynajmniej wiem że jedno zadanko na próbnej dobrze

Eta:

Eta: Masz może linka do tej matury?

Maciess: Nie, sam szukam, ale nigdzie tego nie udostpęnili. Może matura19 nas podratuje

Mila: Teraz Maciess, analizuj sposób Ety, aby zaoszczędzić czas na maturze na trudniejsze zadania.

Eta: https://www.youtube.com/watch?v=FB3KGQJfp4g Znalazłam takie coś

Maciess: Sposób super i dla mnie zrozumiały. Generalnie nie jest biegły w tych zadankach ze stereometrii bo jeszcze nie zabrałem się za nią. Ale generalnie nie mam problemów zeby zmieścić się w czasie na podstawie

Maciess: O super Możemy tu zweryfikowac odpowiedzi?

Maciess: Zad 4. C czy D?

Eta: 4/ D

Eta: https://matematykaszkolna.pl/forum/383405.html Zobacz to bo ten yutuber ......podał bardzo pokrętny dowód ( jak dla mnie

Maciess: Chyba zrobiłem podobnie. Zaznaczyłem podobieństwo trójkątów, zapisałem skale k=1/2 i stwierdziłem że wysokości też mają się jak 1 do 2 a w sumie dają a. Z taką wiedzą można policzyć pola trójkątów tylko znając a. Więc w 3 linijkach wychodziło zadanie.

Eta: Tak trzymaj .....

Maciess: Z tego co patrzyłem to tylko 1 błąd na zamkniętych więc do 100 braknie Możesz mi wytłumaczyć z jakiej własności trapezu skorzystałaś w tym dowodowym z kwadratem? Bo nie bardzo rozumiem

Eta: https://matematykaszkolna.pl/forum/295934.html Wpisz w forumową wyszukiwarkę : Eta trapez"

Eta: Czy już jasne ?

Maciess: oo nie znałem tej własności. Spróbuje to jutro wyprowadzić.

Eta:

Maciess: Dziękuje za pomoc i dobranoc

Eta: Kolorowych snów

Eta: zad 25/ (2x−3)²−4≥0 (bez delty ! |2x−3|≥2 x∊(−∞,1/2>U<5/2,∞) ≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈ i po ptokach