równania i nierówności wielomianowe Sebastian Porowski: Dzień dobry Proszę o sprawdzenie poniższych rozwiązań Rozwiąż równanie/nierówność a)3(x+1)(x−3)³(x+2)²>0 b)x³+3x²−5x−15>/0 c)−x³−6x²−9x=0 d)5x³+11x²=6 Rozwiązania a) x1=−1 ,x2=3,x3=−2 krotności to dla x1 =1 dla x2=3 dla x3=3 i problem pojawia się przy wykresie co dalej? Proszę o sprawdzenie podpunktu a)

Sebastian Porowski: Rozwiązanie dla b) x3+3x2−5x−15>/0 x²(x+3)−5(x+3)>/0 (x+3)(x²−5)>/0 x1=−3 x2=p(5) oraz p−{5} bo mam x²−5>/0

wredulus_pospolitus: (a) ... metoda 'wężyka': https://matematykaszkolna.pl/strona/142.html w sumie to do (b) i każdej innej nierówności stosuje się tą metodę (przyda się ona nawet na studiach o ile tylko będziesz miał jakiekolwiek zajęcia związane z matematyką).

wredulus_pospolitus: spójrz też na rozwiązania przykładowych zadań, np.: https://matematykaszkolna.pl/strona/146.html

Sebastian Porowski: Dzięki wielkie za link już go przeglądam

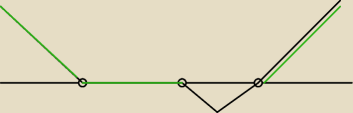
Sebastian Porowski: Tak wygląda mój węzyk pierwsza kropka od lewej to =−2 druga kropka to x1=−1 trzecia kropka to x2=3 z wykresu odczytałem taki x x∊(−∞,−1) U (3,+∞) czy jest to dobre rozwiązanie?

Sebastian Porowski: Proszę o sprawdzenie

Jolanta:

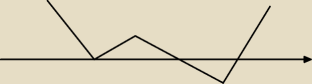
Jolanta: x₁=−1 x₂=3 pierwiastek trzykrotny(do potęgi 3) liczba nieparzysta wykres przechodzi na drugą stronę x₃=−2 pierwiastek dwukrotny (do potęgi 2) liczba parzysta odbicie wykresu

Jolanta: x∊(−∞ :−2) u(−2,−1) u (3;∞)

Jolanta: w b masz > 0 czy ≥0

SEBASTIAN POROWSKI: W B mam te druga opcje

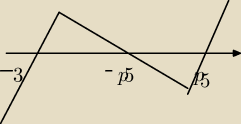
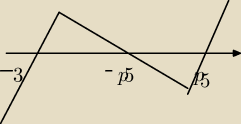Jolanta: znak masz przed oczyma pod napisem powrót do zadań (x−√5)(x+√5)(x+3)≥0 x∊≤−3:−√5≥ u≤√5;∞) gdy piszesz pierwiastek to nawias { }