Proszę o sprawdzenie Wielomiany Sebastian Porowski: Dzień dobry Proszę o sprawdzenie dwóch podpunktów ,które rozwiązałem oraz o pomoc w podpunkcie c) Dane sa wielomiany w(x)=x³+x²−1 q(x) =x−3 u(x)=x²−2x wykonaj działania A) w(x)+q(x)−u(x) B) q(x)*u(x) C) (x³+2x²−x+1) : (x−1) O ile na a i b mam próby rozwiązań to odnośnie c nie mam pomysły. Rozwiązanie a)x³+x²−1+x−3−x²−2x=x³−4−x b)(x−3)*(x²−2x)=x³−2x²−3x²+6x=x³−5x²+6x

wredulus_pospolitus: (c) miałeś schemat Hornera

wredulus_pospolitus: https://matematykaszkolna.pl/strona/1401.html

wredulus_pospolitus: jest to najszybszy sposób na dzielenie wielomianu przed dwumian postaci (x−q)

Sebastian Porowski: Nie miałem ale już się z tym zapoznaje dziękuje za link,po przeanalizowaniu go wrzucę swoje rozwiązanie.

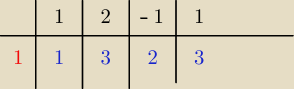
wredulus_pospolitus: dla ułatwienia w tabelce robi się jeszcze jedną kolumnę (na początku) gdzie u dołu (tutaj [C[na czerwono]]) wpisuje się 'q' (w tym przypadku jest to 1) tak więc:

x3 + 2x2 − x + 1		3
	= (x2 + 3x + 2) +
x−1		x−1

wredulus_pospolitus: odnośnie tabelki ... więc robiąc tabelkę do przykładu z linku na czerwono tutaj była by liczba '2' (oczywiście robiąc tabelkę nie będziesz używać kolorów )

Sebastian Porowski: Rozwiązałem to samodzielnie i zastanawia mnie jedno (x²+3x+2) −to wiem skąd się bierze. Jednak zastanawia mnie pochodzenie u{3){x−1} W podanym linku nie istniieje taki zapis i to mnie zastanawia, Wiem,że to pewnie banalne pytanienie ale chcialbym to zrozumiec,

wredulus_pospolitus: zauważ, że zapis w linku wygląda tak: x³ − 4x² + 3x − 5 = (x² − 2x − 1)*(x−2) − 7 .... teraz to obustronnie dzielimy przez (x−2) i otrzymujemy:

x3 − 4x2 + 3x − 5		7
	= (x2 − 2x − 1) −
x−2		x−2

analogicznie w Twoim przypadku.

	x3+2x−x+1
a że masz podać postać:		... to w takiej właśnie to będzie postaci
	x−1

Sebastian Porowski: no i teraz jest wszystko jasne Wracam do kolejnych zadań,które pewnie również wrzucę do sprawdzenia,