Diagram Hassego i antyłańcuchy Elena: Narysuj diagram Hassego minimalnego porządku, przy którym 1 ≼ 2, 2 ≼ 3, 5 ≼ 4, 4 ≼ 2, 6 ≼ 7, 7 ≼ 3, 7 ≼ 8, 8 ≼ 9, 3 ≼ 0, 9 ≼ 0 a) Rozważmy rodzinę niepustych łańcuchów w tym porządku. Ile ma elementów minimalnych, a ile maksymalnych? b) Analogicznie dla rodziny niepustych antyłańcuchów. Czy łańcuchy są to po prostu elementy minimalne i maksymalne a antyłańcuchy−dla maksymalnych−jest to antyłańcuch najdłuższy(składający się z wielu elementów(liczb)) a minimalny to taki,który ma ich najmniej (zazwyczaj pojedyńcze,takie,które nie są w relacji z żadną liczbą np. w tym przypadku 5,1,6? ).Czy w taki sposób należy to rozumieć?

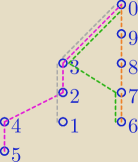
iteRacj@: na diagramie Hassego (dodatkowo) zaznaczyłam różnymi kolorami kilka łańcuchów o największej możliwie długości: 1,2,3,0 5,4,2,3,0 6,7,8,9,0 6,7,3,0 każdy zbiór jednoelementowy jest też łańcuchem

Elena: Rozumiem,czyli maksymalnymi łańcuchami są te składające się z 5 liczb: 5,4,2,3,0 , 6,7,8,9,0 ,ale i również te składające się z 4 liczb czyli 6,7,3,0 oraz 1,2,3,0 ? Natomiast jak rozumieć niepuste antyłańcuchy? To takie elementy,które nie są ze sobą w relacji? Np.maksymalnym antyłańcuchem może być 3,8 lub 5,1,6 ?

Pytający: Tak, wszystkie 4 podane łańcuchy są maksymalne. Maksymalne, czyli nie da się już "dorzucić" do tych podzbiorów żadnego elementu, aby to wciąż był łańcuch (czyli żeby wszystkie elementy były między sobą porównywalne). Antyłańcuchy to takie podzbiory, że każde para elementów jest nieporównywalna między sobą. Przykładowo: {0} jest maksymalnym antyłańcuchem, bo nie można "dorzucić" czegoś nieporównywalnego z 0 {3} jest antyłańcuchem, ale nie maksymalnym (jak "usuniesz" z diagramu Hassego wszystkie elementy porównywalne z 3, znaczy te z łańcuchów fioletowego, szarego i zielonego na rysunku Iteracji, to zostaną jeszcze 8, 9, więc coś można "dorzucić") {3,9} jest maksymalnym antyłańcuchem {3,8} jest maksymalnym antyłańcuchem {2,9} jest maksymalnym antyłańcuchem {2,8} jest maksymalnym antyłańcuchem {2,7} jest maksymalnym antyłańcuchem {2,6} jest maksymalnym antyłańcuchem itd.

Elena: Bardzo dziękuje!

iteRacj@: Pytający Czy możesz napisać, czy relacja z wątku 382082 jest relacją porządku częściowego?

Pytający: Nie jest, dobrze napisałaś. Nie jest ani zwrotna, ani przeciwzwrotna. Tak wygląda diagram tamtej relacji: https://i.ibb.co/rHNs1fj/g1.png

iteRacj@: dziękuję!