punkt przeciecia stycznych tomek3: Sieczna x−y+1=0 przecina okrąg x2+y2−6x−2y+1=0 w punktach A i B. Przez punkty A i B poprowadzono styczne do okręgu, które się przecinają w punkcie C. Napisz równanie okręgu opisanego na trójkącie ABC. mam problem ze znalezieniem wspolrzednych punktu c, czyli przeciecia stycznych, reszta mi idzie sprawnie wiem, ze bylo juz to zadanko tutaj opisywane, ale nie rozumiem odpowiedzi

Mila: Gdzie masz to napisane na forum, może wyjaśnię, albo dam nowe rozwiązanie.

tomek3: https://matematykaszkolna.pl/forum/25671.html

Mila: Dobrze, piszę nowe rozwiązanie.

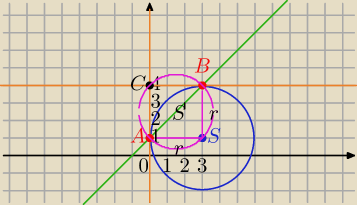
Mila: Sieczna x−y+1=0⇔y=x+1 1) x²+y²−6x−2y+1=0⇔(x−3)²−9+(y−1)²−1+1=0 (x−3)²+(y−1)²=3², S=(3,1), r=3 Rysuję okrąg w układzie współrzędnych i sieczną. 2) Punkty przecięcia: (x−3)²+(x+1−1)²=9 x²−6x+9+x²=9 2x²−6x=0⇔x²−3x=0 x*(x−3)=0 x=0 to y=0+1 Mamy A=(0, 1) (co widać na rysunku ) lub x=3 to y=4 mamy punkt B=(3,4) 3) Styczna jest jest prostopadła do promienia w punkcie styczności i odległa o dł. promienia od środka okręgu. Są dwie proste przechodzące przez A(0,1) i B(3,4) spełniające ten warunek: x=0 ( Oś OY ) i prosta y=4 4) Punkt przecięcia C=(0,4) ΔACB− Δprostokątny równoramienny, |AC|=BC|=3 |AB|=3√2 5) środek okręgu opisanego na Δprostokątnym leży w środku przeciwprostokątnej.

	1		3√2
r=		|AB|=
	2		2

	0+3		1+4		3		5
S'=(		,		)=(		,		)
	2		2		2		2

Równanie okręgu:

	3		5		3√2
(x−		)2+(y−		)2=(		)2⇔
	2		2		2

	3		5		18
(x−		)2+(y−		)2=
	2		2		4

========================== Jeśli dalej nie rozumiesz, to pisz.

tomek3: czyli kluczowe jest tutaj zrobienie rysunku tak naprawde dzieki, wszystko zrozumiale

Mila: Możesz rachunkowo wyznaczyć styczne postaci s: Ax+By+C=0 Korzystasz z wzoru na odległość S od stycznej.

Tojatpy: Moglabys rozwinac?

Mila: S=(3,1) B=(3,4) Odległość punktu S od stycznej równa się 3 s: Ax+By+C=0 i B∊s A*3+B*4+C=0 C=−3A−4B s: Ax+By−3A−4B=0

	|A*3+B*1−3A−4B|
d(S(3,1), s)=3=		⇔
	√A2+B2

|3A+B−3A−4B|=3√A²+B² |3B|=3√A²+B² /² 9B²=9(A²+B²) A=0 s: Ax+By−3A−4B=0⇔ s: By−4B=0 /:B s: y=4

Eta: Jeżeli dany jest okrąg o: (x−a)²+(y−b)²=r² i punkt P(x_P,y_P)∊ do okręgu to styczna w punkcie P ma równanie: (x_P−a)(x−a)+(y_p−a)(y−a)=r² warto to wiedzieć ! ( upraszcza rachunki ) w tym przykładzie A(0,1)∊ o : (x−3)²+(y−1)²=9 styczna w punkcie A ma równanie: (0−3)(x−3)+(1−1)(y−1)=9 3x+9 =9 x=0 (oś Oy−− równanie stycznej stycznej ==============

Eta: styczna w punkcie B(3,4) ma równanie (3−3)(x−3)+(4−1)(y−1)=9 3y−3=9 y=4 −− równanie stycznej ========

Mila: Styczne prawidłowe i prosto obliczone, ale wzór trzeba poprawić. (?)

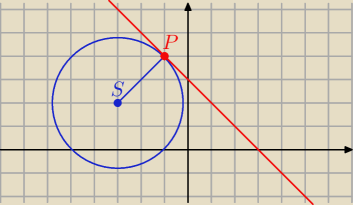
Eta: o: (x+3)²+(y−2)²=8 i P(−1,4) ∊o bo (−1+3)²+(4−2)²= 4+4=8 to styczna w punkcie P ma równanie (−1+3)(x+3)+(4−2)(y−2)=8 2x+6 +2y−4=8 y=−x+3 −−−równanie stycznej ( co zgadza się na rysunku wyżej ========== i nie tracimy cennego czasu na maturze

Eta: Mila gdzie wzór "poprawić" ?

Mila: Ten niebieski .. (y_p−b)*(y−b)....chyba tak liczysz.

Eta: Aaaa no tak z rozpędu nie wpisałam "b" (x_P−a)(x−a)+(y_P−b)(y−b)=r² Dzięki za poprawkę

Mila: Wyciągasz te wzory jak czarodziej z kapelusza Ten mi się podoba.

Eta: W linku wyżej ( 9 lat temu .. Eta =Aza pisała