
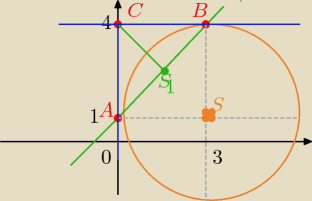
 Rozwiązując układ równań prostej i okręgu wyznaczymy współrzędne punktów A i B
y= x+1 −−− równanie siecznej
x2 +y2 −6x −2y +1=0
x2 +( x+1)2 −6x −2(x+1)+1=0 => 2x2 −6x =0 => x (x −3)=0
to x = 0 v x = 3
więc y= 1 v y = 4 A( 0,1) B(3, 4)
Przekształcamy równanie okręgu : ( x −3)2 +(y −1)2= 9 S( 3,1) r = 3
teraz łatwo napisać równania stycznych
styczna AC: (x−3)*(xA −3) + (y−1)(yA − 1)=9
stycznaBC: ( x −3)(xB −3) + ( y−1)(yB −1)=9
podstawiając współrzędne punktów A i B
otrzymamy:
AC: (x −3)(0−3) + ( y−1)(1−1)=9 => x −3 = −3 => x = 0
AC : x = 0 −−−− to równanie przedstawia oś OY
BC: ( x −3)(3−3) +( y−1)(4−1)=9 => y−1 = 3 => y = 4
BC: y = 4 −−− prosta równoległa do osi OX
zatem punkt przecięcia stycznych to ; C( 0, 4)
zatem trójkąt ABC jest prostokątny , bo kąt C = 90o
i równoramienny bo IACI =IBCI=3
to:
równanie okręgu opisanego na trójkącie ABC można napisać:
Rozwiązując układ równań prostej i okręgu wyznaczymy współrzędne punktów A i B
y= x+1 −−− równanie siecznej
x2 +y2 −6x −2y +1=0
x2 +( x+1)2 −6x −2(x+1)+1=0 => 2x2 −6x =0 => x (x −3)=0
to x = 0 v x = 3
więc y= 1 v y = 4 A( 0,1) B(3, 4)
Przekształcamy równanie okręgu : ( x −3)2 +(y −1)2= 9 S( 3,1) r = 3
teraz łatwo napisać równania stycznych
styczna AC: (x−3)*(xA −3) + (y−1)(yA − 1)=9
stycznaBC: ( x −3)(xB −3) + ( y−1)(yB −1)=9
podstawiając współrzędne punktów A i B
otrzymamy:
AC: (x −3)(0−3) + ( y−1)(1−1)=9 => x −3 = −3 => x = 0
AC : x = 0 −−−− to równanie przedstawia oś OY
BC: ( x −3)(3−3) +( y−1)(4−1)=9 => y−1 = 3 => y = 4
BC: y = 4 −−− prosta równoległa do osi OX
zatem punkt przecięcia stycznych to ; C( 0, 4)
zatem trójkąt ABC jest prostokątny , bo kąt C = 90o
i równoramienny bo IACI =IBCI=3
to:
równanie okręgu opisanego na trójkącie ABC można napisać:
| xA+xB | yA+yB | |||
S1 ( | , | )
| ||
| 2 | 2 |
 dodatkowo czworokąt ACBS jest kwadratem oboku długości 3
Dobrej nocy Wszystkim
dodatkowo czworokąt ACBS jest kwadratem oboku długości 3
Dobrej nocy Wszystkim



 to sprawdzimy ?
1/ x2( 3−x)(x+2)3 >0
i druga troszkę inna ( ale dasz radę
to sprawdzimy ?
1/ x2( 3−x)(x+2)3 >0
i druga troszkę inna ( ale dasz radę  2/ ( x−3)2( x2−4)( 4−x)( x2 −5x+6) ≤0
2/ ( x−3)2( x2−4)( 4−x)( x2 −5x+6) ≤0

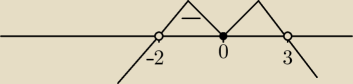 1)x=0 x= 3 x=−2
x∊(−2,3)
1)x=0 x= 3 x=−2
x∊(−2,3)
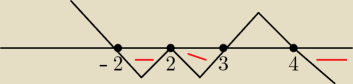 to (x2−5x+6) rozpisalem sobie na (x−3)(x−2)
(x−3)(x−2)( x−3)2( x−2)(x+2)( 4−x)≤0
(x−2)2( x−3)3(x+2)( 4−x)≤0
x=2 x=3 x=−2 x=4
x∊<−2,3>∪<4,∞)
to (x2−5x+6) rozpisalem sobie na (x−3)(x−2)
(x−3)(x−2)( x−3)2( x−2)(x+2)( 4−x)≤0
(x−2)2( x−3)3(x+2)( 4−x)≤0
x=2 x=3 x=−2 x=4
x∊<−2,3>∪<4,∞)


 Świetnie , bardzo się cieszę , zdolny jesteś , nie ma co
Świetnie , bardzo się cieszę , zdolny jesteś , nie ma co No i jak?, łatwiejszy to sposób rozwiązywania , niż poprzedni podawany przez Ciebie?
No i jak?, łatwiejszy to sposób rozwiązywania , niż poprzedni podawany przez Ciebie?





 Aza nigdy nie była na forum a taka matematyczka się z nikąd nie bierze
Aza nigdy nie była na forum a taka matematyczka się z nikąd nie bierze  , a Ty
zmieniasz często nick to odrazu wiedziałem
, a Ty
zmieniasz często nick to odrazu wiedziałem