Algebra - liczby zespolone UczącySię: Siemka, mam takie pytanko: otóż mam graficznie przedstawić zbiór na płaszczyźnie zespolonej Re(z³) ≤ 0 No więc wychodzi oczywiście, że cos3γ ≤ 0, γ ∊ [0,2π]. To w takim razie 3γ ∊ [0,6π]

	π		3π
cos α ≤ 0 ⇔ a ∊ [		+ kπ ,		+ kπ].
	2		2

I tutaj się trochę załamałem rysowanie kiedy cos < 0 itp było w liceum ale tutaj tego nie umiem .. ktoś pomoże ?

UczącySię: Podbiję bo znowu długa cisza ...

UczącySię: Czy ktoś pomoże ?

Blee:

	π		3π
cos a ≤ 0 ⇔ a ∊ [		+ 2kπ ;		+ 2kπ ]
	2		2

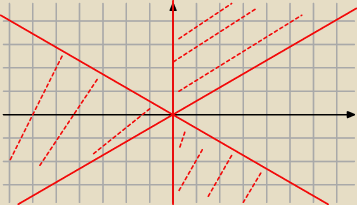
Pytający: cos(3γ)≤0

π		3π
	+2kπ≤3γ≤		+2kπ // 427
2		2

π		2kπ		π		2kπ
	+		≤γ≤		+
6		3		2		3

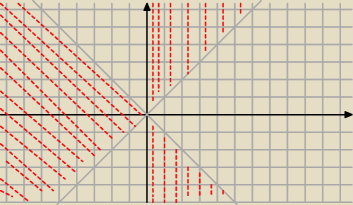
Blee: z³ = x³ + ix²y − xy² − iy³ Re(z³) = x(x² − y²) = x(x−y)(x+y) ≤ 0 1) x ≤ 0 i x ≤ y ≤ −x 2) x ≥ 0 i y ≥ x 3) x ≥ 0 i y ≤ −x

Pytający: Blee, zapomniałeś o współczynnikach. z³ = x³ + 3ix²y − 3xy² − iy³ Re(z³) = x(x²−3y²) = x(x−√3y)(x+√3y)

UczącySię: Ja zapisałem l. zespoloną w postaci trygonometrycznej

UczącySię: Ale dzięki wielkie. Witamy grudzień