Funkcje - zadania misieq: Witam, mam bardzo wielką prośbę odnoszącą się do 12 zadań. Jeśli ktoś miałby chwilę wolnego czasu i mógłby mi jakoś nie zbyt skomplikowanie wytłumaczyć jak rozwiązać każde z tych zadań było by super. Nie chce gotowych odpowiedzi, chciałbym tylko wskazówki jak dane zadanie rozwiązać, żebym mógł sobie to rozwiązać we własnym zakresie. Za wszelką pomoc z góry dziękuje 1 Screen : https://scontent-waw1-1.xx.fbcdn.net/v/t1.15752-9/46634225_180663839552387_7610715437587759104_n.jpg?_nc_cat=105&_nc_ht=scontent-waw1-1.xx&oh=d83db716b0ea7a777e6ae4c8d014c6ef&oe=5C6D441E 2 Screen : https://scontent-waw1-1.xx.fbcdn.net/v/t1.15752-9/46511048_179045659704288_1647762725641650176_n.jpg?_nc_cat=100&_nc_ht=scontent-waw1-1.xx&oh=e68449bf4d458c8598bdfc39f41fedfa&oe=5CAB3D4C

misieq:

misieq: byłoby*

Mila: Później spojrzyj

misieq: Okej

Mila: 1) Funkcja liniowa f(x)=ax+b jest malejąca dla a<0⇒ f(x)=(m−2)*x+2 jest malejąca dla : m−2<0⇔ m<2 ========= 2) Zbiór wartości funkcji: f(x)=−2x²+12x+1 wykresem jest parabola skierowana ramionami w dół. Największą wartość osiąga w wierzchołku; Współrzędne wierzchołka paraboli:

	−b		−12
xw=		=		=3
	2a		2*(−2)

f(3)=−2*3²+12*3+1=19 Z_w=(−∞,19> ============

Mila: 3)f(x)=2x² po przesunięciu o wektor [a,b] otrzymamy wykres funkcji o wzorze g(x)=f(x−a)+b czyli wykres g(x)=2*(x−3)²+5 zatem wykres przesunięty o wektor [3,5] czyli 3 jednostki w prawo i 5 jednostek do góry. =====================

Mila: 4)Nachylenie prostej do osi OX y=√3*x−2 tgα=√3⇔α=60^o ============

	1
5) f(x)=(		)x
	2

Liczysz wartości funkcji: f(−1), f(0), f(2), f(−2)

	1		2
f(−1)=(		)−1=(		)1=21=2
	2		1

A∉wykresu

	1
f(0)=(		)0=1
	2

B∉wykresu

	1		1
f(2)=(		)2=
	2		4

C∉wykresu

	1
f(−2)=(		)−2=22=4⇔
	2

punkt (−2,4) należy do wykresu tej funkcji ================================

Mila: 6) A=(1,2) i f(x)=x²−2x+3m+1 Jeżeli A należy do wykresu tej funkcji to f(1)=2 1²−2*1+3m+1=2 3m=2

	2
m=
	3

======

Mila:

	5
7) f(x)=
	√x2−4

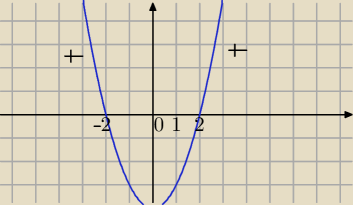
D: x²−4>0 (x−2)*(x+2)>0 x<−2 lub x>2 wybierz odpowiedź

Mila: 8)

	1
f(x)=−		(x−5)2+4
	2

Sprawdzamy czy pierwsza wsp. wierzchołka należy do przedziału <−1,3> x_w=5∉<−1,3> liczysz wartości na końcach przedziału f(−1)= ? f(3)= ? oblicz i wpisz odpowiedź czekam

misieq: Dzięki za poświęcony czas, przysiądę przy tym jutro i napiszę odpowiedzi Dzięki wielkie

Mila: No to reszta jutro.

misieq: 1. Jak jest np y=(m−5)x to funkcja malejąca będzie gdy m<5, a jeśli byłoby np y=(m+5)x to rosnąca to m>5, czy jak? 2. Tutaj w ogóle nie rozumiem tego jak np przenieść funkcje na wykres tzn, jak z funkcji np:f(x)=−2x2+12x+1 narysować parabole. 3. Tylko odczytuje wartości z funkcji np jakby było 2(x−7) + 3 to prawo o 7 góra o 3 tak? 4. Dlaczego akurat tutaj tg przyjęłaś, skoro np w ctgα pierwiastek z 3 to 30 stopni, a tak odp tez jest w podanych? 5. Tutaj podstawiam wartości pod X i patrzę, czy wynik pokrywa się z Y. 6. Tutaj też podstawiam 1 i 2 do funkcji i po prostu liczę. 7. Nie rozumiem na jakiej to działa zasadzie 8. Też nie zbyt wiem co i jak. Jakbyś znalazła chwilę czasu, żeby rzucić światłem na to co napisałem, byłoby super. Pozdrawiam

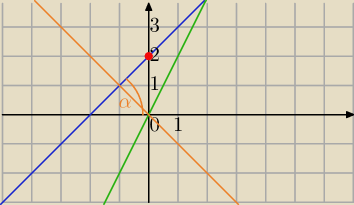
Mila: 1) własności funkcji liniowej: y=ax+b wykresem jest prosta znaczenie współczynników a, b a=tgα, gdzie α− kat nachylenia prostej do osi OX (0,b) − punkt przecięcia osi OY a>0 funkcja jest rosnąca a<0 funkcja liniowa jest malejąca a=0 funkcja stała 1) f(x)=x+2 − funkcja rosnąca a=1, (0,2) punkt przecięcia OY tgα=1, α=45^o Twój przykład y=(m−5)x a) m−5>0 ⇔m>5 funkcja rosnaca , np m=7 y=(7−5)*x, y=2x b) m−5<0⇔m<5 funkcja malejąca, np. m=4 y=(4−5)x⇔y=−x

Mila: Analizuj.(1)

Mila: 3) Tak. 4) masz wyjaśnione w (1) 5) tak 6) tak 2,7,8) Czego nie rozumiesz ? Nie umiesz rozwiązać nierówności kwadratowej? Musisz poznać własności funkcji kwadratowej. −wzór, znaczenie wsp. a, b − współrzędne wierzchołka paraboli − miejsca zerowe −postać kanoniczna, postać iloczynowa Poczytaj to wyjaśnię, co trzeba. w (2) nie potrzeba dokładnego wykresu , wystarczy szkic , ale trzeba wiedzieć jakie są wsp. wierzchołka paraboli.

Mila: https://matematykaszkolna.pl/strona/41.html

misieq: Jak mam postać kierunkową y=ax +b to od a zależy, jaka jest funkcja. np y=(m−3)x+1 jest malejąca to m−3<0 czyli m<3

Mila: funkcja kwadratowa https://www.youtube.com/watch?v=lKZ0gS8f-6k https://matematykaszkolna.pl/strona/3413.html

Mila: 16:59 dobrze.

misieq: Zabieram się za oglądanie.

Mila: Dobrze, to dalej będziemy wyjaśniać:

misieq: 8 f(−1)= −1/2 (−6) +4 = −20 f(3) = −1/2 * 4 + 4 = 2 Czyli odp C=2

misieq: 7 (od − niesk. do −2> v <2 do + niesk.)

misieq: Nie wiem czy dobrze, ale spróbowałem samemu 9 f(x)=2x² − 7x +c Δ=49 = pierwiastek z 7 x1=0 x2=7/2 Czyli c ma wartość 0

Mila: 7,8 OK Następne będę patrzeć

misieq: ostatnich 3 nie mam pojęcia jak zacząć :v

6latek: zadanie nr 9 zle masz f(x)= 2x²−7x+c dwa miejsca zerowe kiedy Δ≥0 Δ= (−7)²−4*2*c (tutaj c ≠1 to jest parametr Δ= 49−8c≥0 −8c≥−49

	49
c≤
	8

misieq: Czyli na takiej zasadzie. Myślałem, że jako C mogę przyjąć 0. Dzięki za poprawienie.

Mila: 9) f(x)=2x²−7x+c Δ>0 ⇔f(x) ma dwa miejsca zerowe. Δ=b²−4ac, a=2, b=−7, wyraz wolny c nie znany Δ=7²−4*c*2 49−8c>0 49>8c

	49		1
c<		=6
	8		8

	49
dla c<		funkcja ma dwa miejsca zerowe
	8

np. c=6 f(x)=2x²−7x+6 Δ=49−4*2*6=1

	7−1		7+1
x1=		lub x2=
	4		4

	6		3
x1=		=		lub x=2
	4		2

10) Podpowiedź y=ax+b a=tgα, a=tg(135^o)=tg(180−45⁰)=−tg(45^o)

misieq: a znak nie powinien być < zamiast ≤ ? Bo delta ma 2 miejsca zerowe kiedy jest wieksza od 0, a nie wieksza/rowna. Chyba ze cos zle zinterpretowałem.

6latek: Nawet przyjales ze c=0 co jest prawda bo wtedy otrzymasz niezupelne rownanie kwadratowe Zupelne jest takie ax²+bx+c=0 niezupelne jest postaci ax²+bx=0 (nie ma wwspolczynnika c lub ax²+c=0 (nie ma wyraz z x

misieq: No okej, czyli zadanie mogę zakończyć zapisując wartość C i nie muszę liczyć miejsc zerowych, tak?

PW: misieq, co ty wygadujesz? (cyt.) Bo delta ma 2 miejsca zerowe kiedy jest wieksza od 0 (!)

Mila: Nie delta a funkcja ma dwa miejsca zerowe: − jeżeli Δ > 0, to funkcja kwadratowa ma dwa miejsca zerowe (trójmian kwadratowy ma dwa różne pierwiastki rzeczywiste, równanie kwadratowe ma dwa rozwiązania rzeczywiste), funkcja przecina oś OX w dwóch punktach: Δ>0 (zapis: delta większa od zera)

misieq: Pw, chodzilo mi o rozwiazania, nie miejsca zerowe. Juz od tego wszystkiego mi sie pogmatwało.

Mila: 9) Nie musisz liczyć miejsc zerowych , nie masz takiego polecenia. Ponadto jakbyś to robił, dla ilu wartości c. rozwiązuj 10.

misieq: tg45=1 y=1 * x +b 0=1 * (−3) +b b=3 y= x + 3

Mila: Źle, przeczytaj dokładnie podpowiedź!

misieq: tg45 = −1 y= −1 *x +b 0=−1 * (−3) + b b= −3 y= −x −3

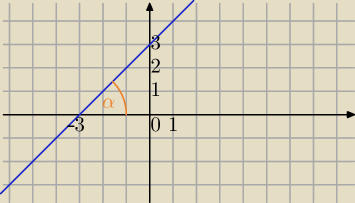
Mila: Oto Twoja funkcja. y=x+3, czy prosta jest nachylona pod kątem 135^o ? Jedno zgadza się z treścią.

misieq: Druga odpowiedź jest poprawna?

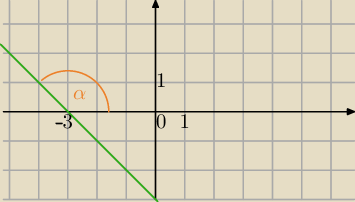
Mila: Teraz dobrze! y=−x−3

misieq: Nie zauważyłem tego minusa po prostu, dziękuję za korektę.

Mila: Teraz rozwiąż najpierw 12) a+2b=20 dalej sam.

Mila: Widzę, że postępy są, musiałeś leniuchować trochę w szkole, albo za dużo randkować, bo masz duże braki

Mila: Rozwiązuj, będę po kolacji na forum.

misieq: a+2b=24 a=24−2b P=a*b P= (24−2b) * b = −2b² +24b y=−2b² +24b Δ24 −24/2 * (−2) = −24/−4 = 6 2b=12 a+12=24 a=12 Wymiary ogródka 12x6

misieq: Powiedzmy, że miałem ciekawsze rzeczy do roboty, a matematyka sama w sobie nigdy mi jakoś szczególnie nie podchodziła. Polski przychodzi mi bez trudu i nie mam najmniejszego problemu z tym przedmiotem. Widocznie nie jestem "ścisłowcem"

misieq: Jeśli będziesz miała jeszcze siłę męczyć się z moją niewiedzą, to możesz zostawić jakąś podpowiedź do zadania nr. 11. Jutro sobie je ogarnę, bo teraz idę obejrzeć coś na netflixie. Spokojnej nocy i dziękuje.

6latek: Zycie nie jest czarno −biale nawyzej bedziesz dobry w tym co lubisz robic bez matury i studiow .

misieq: Maturę myślę, że dam rade ogarnąć na te 30% z matematyki. Od poniedziałku zaczynam korepetycje. Studia natomiast odpuszczam, bo to stanowczo nie dla mnie. Planuję się spełniać w kulturystyce, co poniekąd robię od 3 lat. Pozdrawiam.

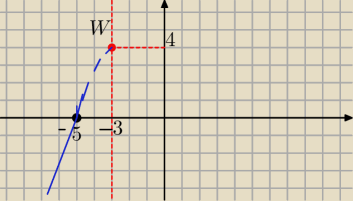
6latek: masz taka sytuacje w zadaniu nr 11

Mila: 11) masz wskazówkę 20:09 W=(−3, 4) wsp. wierzchołka paraboli Napisz f(x) w postaci kanonicznej i wykorzystaj informacje o miejscu zerowym. II sposób Znajdź drugie miejsce zerowe, napisz f(x) w postaci iloczynowej, wykorzystaj informację o współrzędnych wierzchołka paraboli.

6latek: Dobry wieczorMilu

Mila: Jeżeli chcesz być wrakiem w wieku 40 lat to jesteś na najlepszej drodze. ( do tego prowadzi kulturystyka) Zacznij myśleć, zacznij się uczyć, aby mieć przyzwoity zawód z którego są pieniądze i spokojne życie.

Mila: Dobry wieczór Krzysiu

Mila: 12) Masz znaleźć największą wartość funkcji kwadratowej, to po co liczysz deltę ( zresztą źle)? a+2b=24, a=24−2b, a>0 i b>0 ( dlaczego?) 24−2b>0 24>2b i b>0 b<12 i b>0 P(b)=−2b²+24b− parabola skierowana w dół. Największa wartość w wierzchołku:

	−24
bw=		=6
	2*(−2)

b=6 a=24−2*6 a=12m − Wymiary ogródka : 12m x 6m P(6)=−2*62+24*6=−72+144 to samo tradycyjnie P=12m*6m=72m² P(6)= 72m² =================== Musiałam poprawić, zobaczyłam 20 zamiast 24 i powielałam błąd.

PW: Milu (do wpisu z 20:29) − Wiesz oczywiście czym różni się balkon od magistra?

Mila: O już się boję. Nie wiem

Mila: Pozdrawiam i dobranoc

PW: Balkon może utrzymać czteroosobową rodzinę

Mila:

iteRacj@: PW Czy to taka wskazówka dla maturzystów wybierających się na studia? A właściwie dla licealistów, bo technikanci (ładny wyraz) mają luksusową sytuację, mają już zawód.