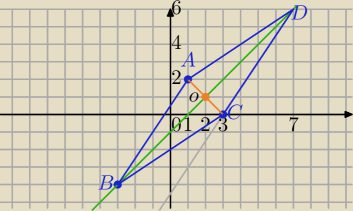
Dane są trzy wierzchołki rombu Alicja: Dane są trzy wierzchołki rombu ABCD:A=(1,2); B=(−3,−4); C=(3,0). Wyznacz rówanie prostej zawierającej przekątną BD tego rombu i równanie boku CD.

the foxi: ba (wektor)=A−B=(1;2)−(−3;−4)=(4;6) cd=ba (wektory) ⇒ D−C=A−B ⇒ D=(A−B)+C=(4;6)+(3;0)=(7;6) prosta przechodząca przez BD 1223 (y+4)(7+3)=(6+4)(x+3) 10y+40=10x+30 10y=10x−10 y=x−1 prosta przechodząca przez CD ... to już sam, wzorując się na przykładzie wyżej i linku

Alicja: Dziękuję

the foxi:

Mila: 1) Wsp.kierunkowy prostej AC: a=−1 BD⊥AC O=(2,1) 2) Prosta BD: y=x+b 1=2+b, b=−1 BD: y=x−1 3) prosta CD||AB AB^→=[−4,−6]

	6		3
wsp. kierunkowy: a=		=
	4		2

Prosta CD:

	3		3		9
y=		x+b, i 0=		*3+b, b=−
	2		2		2

y=(3/2)x−(9/2) 4) Punkt D (3/2)x−(9/2)=x−1 x=7, y=6 D=(7,6) ============