Nierówność logarytmiczna Dbplayer: Rozwiąż nierówność log_4x²(x²−6x+6)≤0

piotr: {4x²>1 ∧ 0<x²−6x+6<=1} ∨ {0<4x²<1 ∧ x²−6x+6>=1}

Tadeusz: zacznij od założeń ... to nie będziesz tego dzielił na te bzdety

ite: @Tadeusz Nawet jak się zapisze najpierw założenia, to i tak dalej trzeba dać takie warunki jak u piotra. Da się tę nierówność rozwiązać w inny sposób? Jaki?

Dbplayer: @ite Może jakaś podpowiedź jaki to sposób

ite: ja widzę tylko taki sposób jaki podał piotr 10:05

Tadeusz: ... przemyśl co piszesz ite z założenia liczba logarytmowana ma być dodatnia zatem x²−6x+6>0 ⇒ x∊(−∞, 3−√3) ⋁ (3+√3, ∞) to niby po co mam zakładać ułamkową podstawę logarytmu

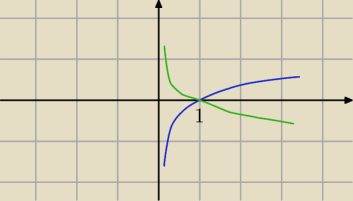
ite: zastanawiałam się nad tym, ale nadal nie widzę błędu o 10:05 są dwie możliwości, żeby otrzymać wynik ujemny gdy funkcja logarytmiczna jest rosnąca {4x²>1 ∧ 0<x²−6x+6<=1} gdy funkcja logarytmiczna jest malejąca {0<4x²<1 ∧ x²−6x+6>=1} gdzie mam błąd

Tadeusz: to nie błąd jeno zbytek łaski ... niby po co mam sprawdzać "wariant" 0<4x²<1

ite: 0<4x²<1

	1
sprawdzam dla np. x=
	4

	1
4x2=		podstawa logarytmu zgodna z def. logarytmu
	4

	1		1		73
x2−6x+6=		−		*6+6=		liczba logarytmowana zgodna z def. logarytmu
	16		4		16

	73
log1/4(		)≈−1,09≤0
	16

	1
czyli należy x=		do zbioru rozwiązań
	4

czemu mamy odrzucać 0<4x²<1 ?

ite: taki sposób rozwiązania zgadza się z wykresem https://www.geogebra.org/classic/bnevccxy zielony wykres, y≤0 liliowy to tylko wykres pomocniczy

ite: 0<4x²<1

	1
0<x2<
	4

	1		1
0<x<		lub −		<x<0 więc należy do podanego przez Ciebie o 14:54 przedziału
	2		2

x∊(−∞, 3−√3) U (3+√3, ∞) i nie wiem dlaczego mam to odrzucić

Jerzy: Tadeusz pokazał, że po zrobieniu założeń zadanie się upraszcza,chociaż niepotrzebnie użył słowa "bzdety"

grzest: Wyznaczenie dziedziny nierówności nie jest przecież równoznaczne z jej rozwiązaniem. http://www.wolframalpha.com/input/?i=log_%7B4x%5E2%7D(x%5E2%E2%88%926x%2B6)%E2%89%A40

PW: ite, skoro już wiesz, że iksy muszą być większe od 3+√3, to po co szukać rozwiązań tam, gdzie ich na pewno nie ma,to jest dla iksów "ulamkowych"?

PW: Z podobną sytuacją miewamy w nierównościach z wartością bezwzględną. Patrz np. 380376 − z góry wykluczamy te wartości parametru p, dla których na pewno nie ma rozwiązań. Dalsze rozwiązanie staje się przez to szybsze.

PW: 380376

iteRacj@: @PW dlaczego, jak piszesz o 20:12, iksy muszą być większe od 3+√3? po zrobieniu założeń 4x²>0, 4x²≠1, x²−6x+6>0

	1		1		1
otrzymuję dziedzinę x∊(−∞,−		) U (−		,0) U (0,		) U (0,3−√3) U (3+√3, ∞)
	2		2		2

i ta część mojego rozwiązania (dla iksów "ulamkowych") należy do dziedziny, to się zresztą zgadza z rozwiązaniem z wolframa z 20:07 jaki popełniam błąd przy wyznaczaniu dziedziny? (mam więcej założeń niż Tadeusz i inny wynik )

PW: Błąd polega na tym, że napisałaś przecinki zamiast "i", co spowodowało taką dziwaczną dziedzinę. Przeczytaj jeszcze raz wypowiedź Tadeusza z 14:54.

iteRacj@: bardzo dziękuję za cierpliwe podejście!

grzest: Przytaczam cytat z wypowiedzi Tadeusza z 14:54: z założenia liczba logarytmowana ma być dodatnia zatem x²−6x+6>0 ⇒ x∊(−∞,3−√3) ⋁ (3+√3,∞) to niby po co mam zakładać ułamkową podstawę logarytmu. koniec cytatu. Na tym nieprawdziwym stwierdzeniu opiera się cała dotychczasowa dyskusja. Nikomu nie przyszło

	1		1
do głowy aby sprawdzić czy rzeczywiście przedział (−		,0)∪(0,		) (na tym przedziale
	2		2

logarytm ma podstawę ułamkową.) jest zawarty w przedziale (−∞, 3−√3)∪(3+√3, ∞) czy też nie. Nawet podanie rozwiązania nierówności z Wolframa nikogo nie zainteresowało i nie skłoniło do refleksji.

	1		1
A przecież [(−		,0)∪(0,		)]⊂[(−∞,3−√3)∪(3+√3,∞)]. Dlatego założenie o ułamkowej
	2		2

podstawie logarytmu jest jak najbardziej zasadne i musi być rozpatrzone.

Iwona75:

	1		1
Czy powinno wyjść x∊(−		,0)∪(0,		)∪<1,3−√3)∪(3+√3,5>?
	2		2

grzest: Tak. Rozwiązanie masz na stronie: http://www.wolframalpha.com/input/?i=log_%7B4x%5E2%7D(x%5E2%E2%88%926x%2B6)%E2%89%A40