rownania rnik: Określ liczbę rozwiązań równania w zależności od parametru m, gdy |5x−4|=|m+3|

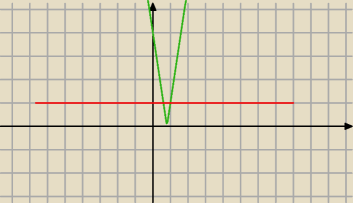
Jerzy: Czerwona: y = |m + 3| Dla |m + 3| = 0 ⇔ m + 3 = 0 ⇔ m = −3 − jedno rozwiazanie Dla |m +3| ≠ 0 ⇔ m ≠ − 3 − dwa rozwiazania

rnik: Dziękuję bardzo. A w jaki sposób poradzić sobie z takim zadaniem: Dla jakich wartości parametru p równanie

	2
|		+3|=p2−1 ma dwa rozwiązania różnych znaków? Wiem jak narysować wykres wyrażenia po
	x+1

lewej stronie, ale co z prawą? w odpowiedziach mam podaną wskazówkę, że warunki zadania są spełnione, gdy p²−1>3 i p²−1<5, ale skąd to się wzięło?

PW: Mamy do czynienia z równaniem typu |u|=p²−1. Aby miało ono jakiekolwiek rozwiązanie, musi być p²−1≥0 − wynika to z definicji wartości bezwzględnej (lewa strona równania jako wartość bezwzględna musi być nieujemna). Dla takich p rozwiązaniami równania są: u = −(p²−1) lub u= p²−1. Mamy więc do rozwiazania dwa równania:

	2
(a)		+3=−p2+1, p2−1≥0
	x+1

lub

	2
(b)		+3=p2−1, p2−1≥0.
	x+1

Rozwiąż spokojnie (a) oraz (b) nie przejmując się wskazówką z książki.

rnik: Ooo, dziękuję bardzo!