Znajdz rozwiazanie nierownosci . Prosze o pomoc justoneeee: |x+3|+|x−2|+|1−3x|−|x+5|≥0

Jerzy: Trzeba rozwiązywać w przedziałach.

justoneeee: Nie miałam przedziałów. Mógłby mi ktoś wytłumaczyć?

Kacper: No to jak nie miałaś, to nie ma sensu tłumaczyć

justoneeee: Ale rozwiązać trzeba jakoś

Jerzy: A może znasz definicję wartości bezwzględnej ?

justoneeee: X dla x≥0 −x dla x<0

Jerzy: I o to chodzi.... np: |x + 3| = x + 3 dla x + 3 ≥ 0, ale = −x − 3 dla x + 3 < 0 Teraz ustal jak będą wyglądał wszystkie moduły w tym równaniu dla x < −3 ?

justoneeee: 2x+2?

Jerzy: Zacznijmy od x < − 5 | x + 3 | = −x − 3 | x − 2| = ?

justoneeee: −x+2

konrad:

Jerzy: Następny moduł ?

justoneeee: −1+3x X+5

Inka: https://matematykaszkolna.pl/strona/1653.html

Jerzy: Nie....popraw.

justoneeee: −x−5

Jerzy: Tak .... i jeszcze poprzedni.

Jerzy: Teraz podstaw te wszystkie wartości do nierówności ( bez modułów ) i rozwiązuj ją w przedziale (−∞,−5)

justoneeee: −1+3X

Jerzy: Nie , przecież liczba pod modułem jest dodatnia dla x < −5

justoneeee: −x−3−x+2−1+3x+x−5≥0 X≥7/2

konrad: ...+1−3x+x+5≥0

justoneeee: A czemu 1−3x?

konrad: Jerzy wyżej napisał.

justoneeee: Ok

Jerzy: Potem zrobisz to samo dla przedziału <−5,3)

Jerzy: <−5;−3) miało być.

konrad: niech może najpierw dokończy rozwiązanie dla tamtego przedziału

justoneeee: −x−3−x+2+1−3x+x+5≥0 −4x+5≥0 X≤5/4

konrad: ok, teraz jeszcze musisz wyznaczyć część wspólną rozwiązania i przedziału w którym rozwiązywałaś

justoneeee: −∞,5/4

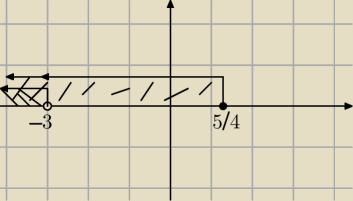
konrad: no, nie bardzo /

konrad: sorry za rysunek

justoneeee: Dobra matematyka nie jest dla mnie

justoneeee: A przedział był (−∞,−5) to dlaczego −3?

konrad: kurde, sorry, tak −5 ,nie −3

konrad: no to jaka będzie część wspólna (−∞,−5) i (−∞,5/4) ?

justoneeee: (−∞,−5)

konrad:

konrad: no i teraz robisz jeszcze raz od początku dla pozostałych przedziałów

justoneeee: Czyli przedział <−5,−3) −−x−3−x+2+1−3x−x−5≥0?

justoneeee: Bez jednego minusa z przodu

konrad: tak

jc: Nie będzie to (−∞, 1/4] U [1/2,∞) ?

justoneeee: <−3,1/3) x+3−x+2+1−3x−x−5≥0 (1/3,2> x+3−x+2+1+3x−x−5≥0 (2,∞) x+3+x−2−1+3x−x−5≥0 Tak reszta? Dobre przedzialy?

qwerty: jc, będzie, znalazłeś jakiś ciekawszy sposób niż przedziały?

jc: To zadanie na wytrwałość. |x+3|+|x−2|+|1−3x|−|x+5|≥0 Podstawmy x=1/2. 3+1/2 + 3/2 + 1/2 − 5 − 1/2 = 0 x=1/4 3+1/4+2−1/4+1/4−5−1/4=0, Każde rozwiązanie powinno te dwie liczby uwzględniać.

jc: Dla x ≥ 1/3 mamy |x+3|+|x−2|+|1−3x|−|x+5| = 2x−1 Dla x ≤ 1/3 mamy |x+3|+|x−2|+|1−3x|−|x+5| = 1−4x. Jak to sprawdzić?