Nierownosci w ukladzie Krzysiek60: narysuj w ukladzie wspolrzednych zbior punktow ktorych wspolrzedne (x,y) spelniaja nierownosc 1) x²+y²≤2x+4y−5 Patrze tak na to i moze tak x²−2x+y²−4y+5≤0 x²−2x+1 + y²−4y+4≤0 (x−1)²+ (y−2)²≤0 Wyszlo mi rownanie kola o promieniu 0 wiec to bedzie w ukladzie punkt (1,2)? 2) 3x²+8y²+14xy>0 Tutaj nie wiem jak to rozlozyc

Bleee: A) tak B) (3x + 2y)(x + 4y) > 0 Na początek zrób... =0 Zauwaz że wtedy to równanie prezentuje dwie proste przecinajace się. Natomiast kiedy będzie iloczyn > 0 wtedy gdy będziemy poniżej obu prostych bądź powyżej obu prostych

Krzysiek60: Czesc. Tylko ze ja nie wiem jak doprowadzic do tej postaci .

jc: Krzysiek, a potrafiłbyś gdyby y było równe jeden? 3x²+14x+8 = iloczyn

Krzysiek60: Witaj tak wtedy

	2
3(x+		(x−4)= (3x+2)(x−4)
	3

jc: Popraw i zobacz, co by było, gdyby było y.

Krzysiek60:

	2
Mialo byc 3(x+		)(x+4) = (3x+2)(x+4)
	3

Krzysiek60: Zaraz A gdybym to rownanie rownanie rozwiazal tak 3x²+14xy+8y² a=3 b= 14y c= 8y² Δ= 100y² √100y²= 10y y₁= −4y

	2
y2=−		y
	3

	2
3x2+14y+8y2= 3(x+		y)(x+4y)= (3x+2x)(x+4y)
	3

Krzysiek60: Mam dwie proste 3x+2y=0 i x+4y=0 Juz sobie dam rade . dzieki

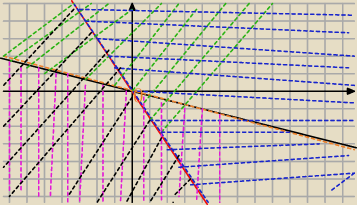
Krzysiek60: jednak mam pytanie Zbior rozwiazan to cala plaszczyzna oprosz tych prostych A co z punktem (0,0) ? jest to przeciecia sie tych prostych wiec nalezy do nich a skoro nalezy do nich to nie nalezy do rozwiazania Dobrze rozumuje ?

Jerzy: Cześć To nie jest cała płaszczyzna. Weż np. punkt (−2;1). Przemyśl jescze raz. Co do punktu (0,0) , to oczywiście nie należy on do zbioru rozwiazań

Krzysiek60: Dzien dobry Jerzy Wylaczylem te proste z rozwiazania .

Krzysiek60: Jeszcze mam prosbe do Ciebie Prosze zobacz tutaj https://matematykaszkolna.pl/forum/379641.html

Jerzy: Ale to nie jest cała płaszczyzna. Podalem Ci przykład punktu (−2,1) , ktory nie spełnia zadanej nierowności

Krzysiek60: Dobrze Jerzy Narysuje sobie to jeszcze raz ale potem bo teraz cos sie zle poczulem . Prosze sprawdz jeszce tamto zadanie

Jerzy: Twoje rozwiązanie jest prawidłowe.

Blee: Krzysiek ... napisałem Ci na początku: 1) obszar POWYŻEJ obu prostych 2) obszar PONIŻEJ obu prostych Obszar 'pomiędzy' (i oczywiscie same proste) NIE NALEŻĄ do rozwiązania

Blee: Dlaczego? Bo wtedy 'jeden nawias' będzie dodatni, a drugi ujemny (więc w konsekwencji iloczyn będzie ujemny)

Krzysiek60: 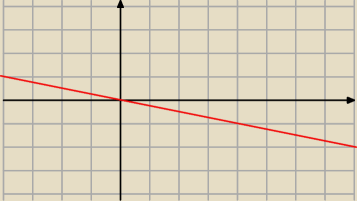Blee ja pozniej postaram sie to zrobic . na razie tylko ogladam i sie nie udzielam bo dobija mnie cukier

Jerzy: Krzysztof: Jak napisał Blee ... tylko punkty leżące nad obydwoma prostymi lub pod obydwoma prostymi.

Krzysiek60: Juz to rozumiem mam juz to w zeszycie narysowane dzieki za pomoc