Nierowność Meto: Hej potrzebuje pomocy, ponieważ wychodzi mi nieprawidłowy wynik i niezbyt wiem dlaczego. Jakby ktoś mógł rozwiązać byłbym wdzięczny 7^x−9*7^−x+8>0

Blee: to pokaż swoje obliczenia

Blee: to co masz można zapisać jako:

1
	(7x − 8)(7x − 1) > 0
7x

Krzysiek60: Albo tak

	1
7−x=
	7x

7^x=t i t>0 (dlaczego ?

	9
t−		+8>0
	t

dalej Ty potem wracasz do podstawienia

Meto: ja rozpisałem to tak: t=7^x t−9*1/t+8>0 /*t t²−9+8t>0 t²+8t−9>0 i liczę deltę, ostatecznie wychodzi t1=−9, t2=1 t∊(−∞;−9)∪(1;∞) a odpowiedz powinna być inna

Krzysiek60: Pewnie ze inna

Blee: bo nie masz założenia ... t > 0 A dlaczego powinno być takie założenie ... teraz sobie odpowiedź na to pytanie

Meto: bo nie można dzielić przez 0 ? Wtedy równie dobrze może być t<0

Krzysiek60: Bzdury kazesz gosciu Popatrz na wykres funkcji wykladniczej i zobacz jakie przyjmuje wartosci

Meto: możecie mi to proszę rozpisać i sam znajdę sobie błędy ?

Krzysiek60: Ne ma sensu rozpisywac dopoki nie odpowiesz na pytanie ktore Ci zadano

Meto: dlaczego t>0 ? nie wiem. to jest moja odpowiedź

Krzysiek60: https://matematykaszkolna.pl/strona/187.html Widac z ezarowno dla a>0 i a∊(0,1) funkcja przyjmuje tylko wartosci dodatnie (ani 0 ani ujemnych ) Teraz wiadomo dlaczego nalezy przyjac zalozenie ze t>0?

Meto: no dobra, ale co to zmienia w sprawie z deltą ? Mam odrzucić wszystkie ujemne wartości z przedziału ? Sprawdzam sobie na photomath i tam delta została rozpisana na 2 rodzaje równanie >0 i t>0 równanie <0 i t<0 i z tego wyszedł ogólny przedział tylko niezbyt rozumiem czemu

Blee: t<0 <−−− na pewno nie tak zauważ, że jeżeli Δ<0 to równanie t² +8t −9 = 0 NIE MA rozwiązań i z całą pewnością doskonale wiesz, że w tym momencie (o ile tylko) a>0 to t² +8t −9>0 jest ZAWSZE (zawsze = wtedy gdy Δ<0) spełniona

Mila: 7^x−9*7^−x+8>0⇔

	1
7x−9*		+8>0
	7x

7^x=t , t>0

	9
t−		+8>0 /*t
	t

t²+8t−9>0 Δ=100

	−8−10		−8+10
t=		=−9 ∉D lub t=		=1
	2		2

(t<−9 lub t>1) i t>0⇔ t>1 7^x>1 7^x>7⁰ x>0

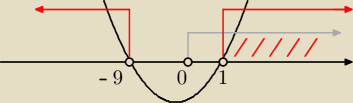
Maciess: t>0 ! Miejsca zerowe dobrze wyliczyłeś i teraz ustalasz częśc wspólną z waurnkiem zmiennej pomocniczej. Wychodzi nam że t∊(1,+∞) t>1 7^x>1 7^x>7⁰ x>0

Meto: zabijcie mnie, ale dalej nie rozumiem czemu musi być t>0, chodzi o to, że 7^x nigdy nie da wartości 0 lub mniej ? Jeżeli nie i ktoś potrafiłby do wytłumaczyć najprostszymi słowami

Blee: BO FUNKCJA f(x) = 7^x jest ZAWSZE dodatnia

Blee: tak samo jak robisz podstawienie t = sinx to piszesz: t∊<−1 ; 1>

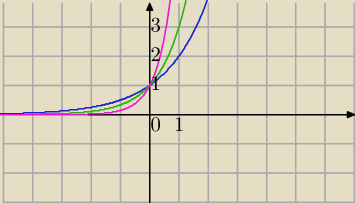
Mila: Oto wykres funkcji: y=2^x y=3^x y=7^x Nie chodziłeś do szkoły, gdy przerabiano funkcję wykładniczą?

Mila: Funkcja wykładnicza. https://eszkola.pl/matematyka/funkcja-wykladnicza-5204.html