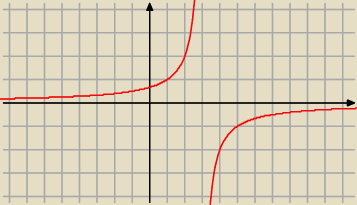
Zbadaj monotonicznosc funkcji Tomal: Zbadaj monotonicznosc funkcji f(x) ²_3−x w przedziale (3,∞) f(x)= ^2x−3_x+1 Prosze o pomoc

Tadeusz: monotoniczność funkcji wymiernej ... zależność od a

Tomal: Jestem w 2 klasie liceum, nie wiem co to funkcja wymierna

Fajter: Wyrazenie wymierne jest to iloraz dwoch wielomianow Ale tego nie musisz wiedziec zeby zbadac monotonicznosc funkcji funkcja jest rosnaca jesli x₁<x₂ to f(x₁)<f(x₂) wiec x₁−x₂<0 to f(x₁)−f(x₂)<0 Funkcja jest malejaca jesli x₁<x₂ to f(x₁)>f(x₂) wiec x₁−x₂<0 to f(x₁)−f(x₂)>0 wybieraj ktorys zapis i badaj znak

Krzysiek60: https://matematykaszkolna.pl/forum/378586.html tutaj byla wymierna wiec?

Krzysiek60:

	2
f(x)=
	3−x

x₁<x₂ to x₁−x₂<0 f(x₁)< f(x₂) to f(x₁)−f(x−2)<0

2		2		2(3−x2)−2(3−x1)		6−2x2−6+2x1
	−		=		=		=
3−x1		3−x2		(3−x1)(3−x2)		3−x1)(3−x2)

−2x2+2x1		2(x1−x2)
	=
(3−x1)(3−x2)		(3−x1)(3−x2)

Analiza x∊(3,∞) wobec tego licznik <0 z zalozenia Mianownik . mamy iloczyn dwoch liczb ujemnych wiec jest dodatni >0 Caly ulamek <0 czyli f(x₁)−f(x₂)<0 czyli funkcja rosnaca cow idac na wykresie Druga rob sam

Krzysiek60: Druga musisz badac w dwoch przedzialach x∊(−∞,−1) i x∊(−1,∞)