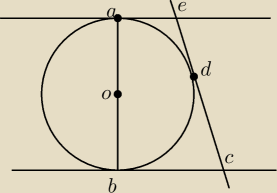
 W końcach średnicy okręgu poprowadzono styczne do okręgu i przecięto je trzecią styczną do tego
okręgu (rysunek obok). Wykaż, że iloczyn długości odcinków AE i BC jest równy kwadratowi
promienia okręgu.
W końcach średnicy okręgu poprowadzono styczne do okręgu i przecięto je trzecią styczną do tego
okręgu (rysunek obok). Wykaż, że iloczyn długości odcinków AE i BC jest równy kwadratowi
promienia okręgu.
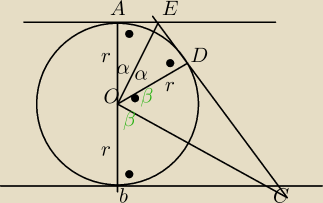 trójkąty AEO i EOD są przystające i podobne do BCO i COD, podobne gdyżβ=90−α
trójkątyBCO i COD są przystające
AE/r=r/BC
AE*BC=r2
cnu
trójkąty AEO i EOD są przystające i podobne do BCO i COD, podobne gdyżβ=90−α
trójkątyBCO i COD są przystające
AE/r=r/BC
AE*BC=r2
cnu
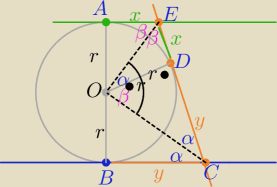 Bardzo podobnie jak podaje a7
1/ z tw. o odcinkach stycznych |AE|=|ED|=x i |BC|=CD|=y
z podobieństwa trójkątów OCD i ODE :
Bardzo podobnie jak podaje a7
1/ z tw. o odcinkach stycznych |AE|=|ED|=x i |BC|=CD|=y
z podobieństwa trójkątów OCD i ODE :
| y | r | |||
= | ⇒ r2=x*y=|AE|*|BC| | |||
| r | y |