Niby proste równanie
Kraterek: Maszeruje oddział żołnierzy. Głębokość szyku (odległość od pierwszego do ostatniego żołnierza)
wynosi 20 m. Od pierwszego żołnierza odbiegł pies, dobiegł do ostatniego żołnierza, zawrócił i
dobiegł znów do pierwszego. W czasie gdy pies biegał, żołnierze przeszli 20 m. Jaką odległość
przebiegł pies?
25 wrz 12:07
Kraterek: Czy ktoś ma pomysł?
25 wrz 13:14
25 wrz 13:16
Kraterek: Po prostu 40 m? Wydaje mi się, że to trudno policzyć − brakuje jakiejś informacji o prędkości.
25 wrz 13:19
Bleee:
Nie będzie to 40 metrów. Bo by to oznaczało że biegnąc od pierwszego do ostatniego żołnierza
pokonuje pies drogę 10 metrów i taka sama w tym czasie pokonuje kolumna, więc podążają z tą
samą prędkością, więc pies nigdy nie dogoni pierwszego żołnierza.
Natomiast jeżeli pies podąża dwukrotnie szybciej niż kolumna to pokonuje on łącznie drogę
20*(2/3) + 20*(5/3) co jest odległościa większą niż 40 metrów i dodatkowo − − − nie zdąży
dogonić pierwszego żołnierza nim kolumna przejdzie 20 metrów.
25 wrz 14:54
Bleee:
Robimy tutaj proporcje:
Gdzie x to droga jaka przebiegł pies od pierwszego do ostatniego,
a całkowita przebywa trasa przez psa wynosi 20+2x
x
2 = 400 − x
2
x
2 = 200
x = 10
√2
Wiec pies przebył drogę 20(1+
√2)
25 wrz 15:04
Bleee:
Autorze... zastanów się skąd taka proporcja, jak nie wiedział to się odezwij
25 wrz 15:06
PW: Nie jestem fizykiem, ale może trzeba pomyśleć tak:
Gdyby stary mądry pies położył się i poczekał aż ostatni żołnież zrówna się z nim, po czym
oddział zrobi "w tył zwrot" i przemaszeruje z powrotem, to pierwszy żołnierz pokona względem
nieruchomego psa dystans 2×20 m = 40 m.
Trzeba odpowiedziec na pytanie:
− Czy łączny dystans między psem a pierwszym żołnierzem zmieni się, jeżeli najpierw pies
pobiegnie "w tę", a potem "we w tę"? Na pewno
prędkości przemieszczania się psa względem
pierwszego żołnierza będą dwie różne, ale czy łączna przebyta droga?
Zadanie okazało się trudne, więc proszę się nie naśmiewać

25 wrz 15:35
Bleee:
PW ale tu fizyka nie ma znaczenia, to zadanie jest analogiczne do zadania:
Dla jakiego x trójkąty prostokątne (o przyprostokatnych x i 20−x oraz 20+x i x) będą podobne
25 wrz 18:37
Bleee:
Spójrz jaka ja proporcje zrobiłem.
25 wrz 18:38
Kraterek: Bleee Próbuję to rozrysować, chyba Twoje rozwiązanie ma sens, ale jeszcze nie wiem
dokładnie czy wszystko rozumiem, będę rozgryzać dalej

W każdym razie dzięki.
26 wrz 12:49
Blee:
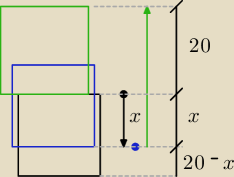
I porównujemy:
| ⎧ | = x/(20−x) ; w pierwszym etapie poruszania | |
| ⎩ | = (20+x)/x ; w drugim etapie poruszania |
|
26 wrz 12:59
Blee:
masz rysunek (wcześniej nie mogłem go dać, bo pisałem z komórki)
26 wrz 12:59
Kraterek: Blee A czy czasem pies nie przebiegł na drugim etapie 20−x+20=40−x? Musiał dobiec znów
do ostatniego żołnierza, który w tym czasie przemieścił się o 20−x i potem jeszcze na czoło
kolumny czyli 20.
A w ogóle to nie wiem czy bez danych prędkości można to rozwiązać.
26 wrz 19:21
PW: No trudne ci jest

.
Blee ma rację, ale nie umiem sam sobie tego "po swojemu"
wytłumaczyć.
Już posunąłem się do przykładu: prędkość oddziału 2 m/s, a prędkość psa 4,95 m/s (dane zgodne z
fizjologią) i prawie się zgodziło.
Tyle że w zadaniu nie ma żdanych danych poza tym, że pies biegał dopóki oddział nie przeszedł
20 m (i akurat wtedy dobiegł z powrotem do pierwszego żołnierza).
26 wrz 19:52
Bleee:
Karatek
1) pies biegnie od pierwszego do ostatniego żołnierza i biegnie tak x metrów, w tym czasie
kolumna poruszyła się o 20−x metrów (tak by ich łączna droga dała 20 metrów, czyli długość
kolumn
) − − − patrz niebieski kwadrat
2) pies biegnie teraz w tą samą stronę co kolumna... Kolumna poruszy się o brakującą liczbę
metrów czyli dokładnie o x metrów (bo 20 = (20−x) + x), natomiast pies poruszył się o 20+x
metrów (droga która przeszła kolumna + długość kolumny)
2) innymi slowy: pies był x metrów od punktu startowego pierwszego żołnierza (przed
rozpoczęciem ruchu), wiemy że pierwszy żołnierz ostatecznie znajdzie się 20 metrów od
początkowego miejsca, więc pies musiał przebiec 'stracone' x metrów a następnie te 20 metrów.
Mam nadzieję że trochę rozjasnilem
27 wrz 00:34
PW:
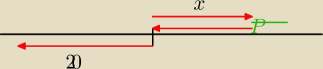
Niech x oznacza drogę przebytą przez psa do momentu, gdy zrówna się z ostatnim żołnierzem
podążającym w przeciwnym kierunku.
Pies przebiegnie 2x+20 (dwukrotnie drogę x oraz 20 m jakie przejdzie pierwszy żołnierz od
momentu startu).
Postaramy się obliczyć x, wiedząc że w pewnym czasie t
1 (od momentu startu do spotkania psa z
ostatnim żołnierzem) pies przebiegł drogę x, zaś ostatni żołnierz zieloną drogę (20−x):
skąd
Po podzieleniu obu stron równania przez t − czas od momentu startu do końcowego spotkania psa z
pierwszym żołnierzem − otrzymamy
| | x | | 20−x | |
|
| = |
| |
| | t.Vpsa | | t.Voddziału | |
czyli
Równanie to jest równoważne równaniu
20x=40x−2x
2+400−20x
x
2=200
x=10
√2
Odpowiedź: Pies przebiegł 2x+20 = 20
√2+20=20(
√2+1} czyli ok. 48,28 m.
Blee zrobił to z talentem, ja musiałem się podeprzeć w sposób jawny pojęciami
"droga−prędkość−czas", ale nareszcie zrozumiałem.
Z pokorą przyznaję, że często problem wydaje się łatwiejszy niż jest i popełniamy fatalne błędy
378144 (mówię o sobie).
27 wrz 12:18
ite:
jako autorka nieprawidłowej odpowiedzi z wątku 378144 też przyznaję, że łatwo jest
popełnić błąd
27 wrz 14:08

 W każdym razie dzięki.
W każdym razie dzięki.
 I porównujemy:
I porównujemy:
 . Blee ma rację, ale nie umiem sam sobie tego "po swojemu"
wytłumaczyć.
Już posunąłem się do przykładu: prędkość oddziału 2 m/s, a prędkość psa 4,95 m/s (dane zgodne z
fizjologią) i prawie się zgodziło.
Tyle że w zadaniu nie ma żdanych danych poza tym, że pies biegał dopóki oddział nie przeszedł
20 m (i akurat wtedy dobiegł z powrotem do pierwszego żołnierza).
. Blee ma rację, ale nie umiem sam sobie tego "po swojemu"
wytłumaczyć.
Już posunąłem się do przykładu: prędkość oddziału 2 m/s, a prędkość psa 4,95 m/s (dane zgodne z
fizjologią) i prawie się zgodziło.
Tyle że w zadaniu nie ma żdanych danych poza tym, że pies biegał dopóki oddział nie przeszedł
20 m (i akurat wtedy dobiegł z powrotem do pierwszego żołnierza).
 Niech x oznacza drogę przebytą przez psa do momentu, gdy zrówna się z ostatnim żołnierzem
podążającym w przeciwnym kierunku.
Pies przebiegnie 2x+20 (dwukrotnie drogę x oraz 20 m jakie przejdzie pierwszy żołnierz od
momentu startu).
Postaramy się obliczyć x, wiedząc że w pewnym czasie t1 (od momentu startu do spotkania psa z
ostatnim żołnierzem) pies przebiegł drogę x, zaś ostatni żołnierz zieloną drogę (20−x):
Niech x oznacza drogę przebytą przez psa do momentu, gdy zrówna się z ostatnim żołnierzem
podążającym w przeciwnym kierunku.
Pies przebiegnie 2x+20 (dwukrotnie drogę x oraz 20 m jakie przejdzie pierwszy żołnierz od
momentu startu).
Postaramy się obliczyć x, wiedząc że w pewnym czasie t1 (od momentu startu do spotkania psa z
ostatnim żołnierzem) pies przebiegł drogę x, zaś ostatni żołnierz zieloną drogę (20−x):