Prosze o rozwiazanie tego zdanka Dawid: Rozważmy dwie proste L1, L2 odpowiednio o równaniach y=0, y+x=0. Niech M oznacza zbiór tych punktów, których odległość od prostej L2 jest dwa razy mniejsza od odległości od prostej L1. Zbiór M składa się z dwóch prostych. Wskaż wszystkie te proste, które zawierają się w zbiorze M

Blee: Na pewno jest 'dwa razy mniejsza' ? Jeżeli tak to ... nie istnieje ani jedna taka prosta, która zawiera się w zbiorze rozwiązań

Dawid: takie sa odpowiedzi A. y=√2*x/1−√2 B. y=−√2*x/1+√2 C. y=2x/3 D. y=(√2+1)*x Może być kilka poprawnych odpowiedzi. A treść jest dobra

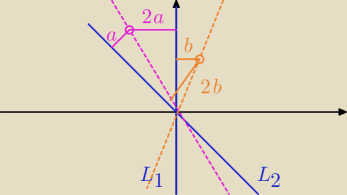
ite: może w ten sposób szukać...

ite: właśnie zauważyłam, że na moim rysunku L₁ ma wzór x=0 rysunek do niczego, ale pomysł może się przydać

PW: Ale narysowałaś odległości od prostej x=0 zamiast y=0.

PW: Nic nie mówiłem

ite: dopiero się uczę...

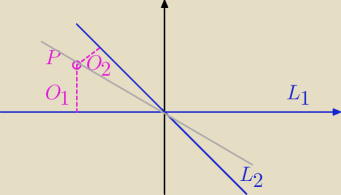
ite: szukamy równania prostej L₃ utworzonej przez punkty spełniające warunek 2*O₂=O₁ odległość P(x_o,y_o) od prostej L₁: y=0 O₁ = |y_o| odległość P(x_o,y_o) od prostej L₂: x+y=0

	|1*xo+1*yo|
O2 =		wzór 1249
	√12+12

stąd

	|1*xo+1*yo|
|yo| = 2*
	√2

|y_o| = √2*|x_o+y_o|

iteRacj@: Rozwiązaniem równania są dwie proste:

	√2*x		−√2*x
y=		oraz y=
	1−√2		1+√2

i one tworzą zbiór M .