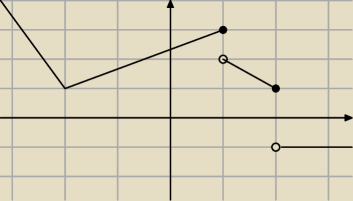
Monotoniczność funkcji D4n1s0: Poniżej przedstawione są wykresy pewnych funkcji. Podaj maksymalne przedziały monotoniczności. Moja odpowiedź: Funkcja malejąca: (−∞; −2> , (1, 2> Funkcja rosnąca: <−2, 1> Funkcja stała: (2, +∞) W podręczniku: funkcja malejąca (ta druga) ma przedział zamknięty: <1,2> Z innymi przykładami podobnie. (mam inny rodzaj przedziału) Liczby zmieniłem pod rysunek. Mógłby mi ktoś wyjaśnić "na chłopski rozum" jak ustala się tu przedziały monotoniczności?

iteRacj@: spójrz na wykres: f(1) jest większa niż wartość dla jakiejkolwiek liczby z przedziału (1, 2> oraz tak jak napisałeś funkcja jest malejąca w przedziale (1, 2> więc jeśli masz podać maksymalny przedział, w którym f(x) maleje to będzie <1, 2>

D4n1s0: A dlaczego tak nie jest z funkcją stałą, f(2) też ma większą wartość niż jakakolwiek liczba z przedziału (2,+∞)

iteRacj@: Decyduje to, co się dzieje w tym przedziale. Funkcja dla żadnej z liczb z przedziału (2,+∞) nie ma wartości większej niż dla którejkolwiek liczby następnej po niej, więc w tym przedziale nie jest spełniony warunek definicji f.malejącej 26. Dołączenie do przedziału liczby 2 tego nie zmienia. Inaczej mówiąc, nie chodzi o to, żeby tylko pierwsza wartość funkcji w przedziale był większa od każdej następnej z tego przedziału, ale o to, żeby po każdej wartości funkcji następowały już tylko wartości mniejsze od niej.

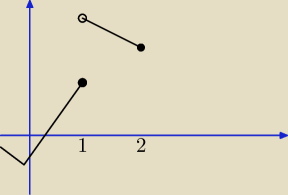
iteRacj@: jeszcze uwaga do pytania z 14:41 np. w takiej sytuacji nie możemy dołączyć do przedziału, w którym funkcja jest malejąca (1, 2> liczby 2.

iteRacj@: liczby 1 oczywiście

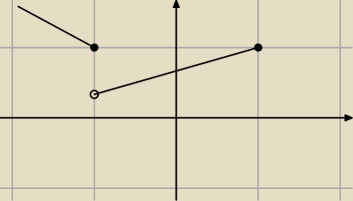
D4n1s0: Ale dołączamy te liczby tylko gdy funkcja jest malejąca? Chyba głupieje, serio, nie czaje. Czyli jak funkcja jest rosnąca (na rysunku) to tej liczby już nie dołączamy, czyli przedział (−1,1>?

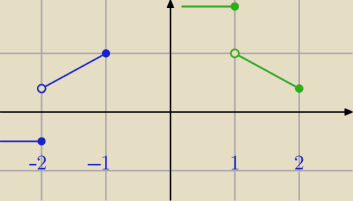
iteRacj@: może rysunki pomoże zobaczyć na czym to polega: tutaj w obu sytuacjach dołączamy liczbę do następującego po niej przedziału otwartego, więc maksymalny przedział, w którym f(x) rośnie to będzie <−2,−1> a maksymalny przedział, w którym f(x) maleje to będzie <1, 2>

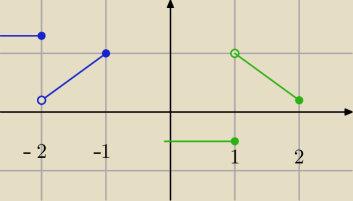
iteRacj@: tutaj w obu sytuacjach nie dołączamy liczb do następujących po nich przedziału otwartego, więc maksymalny przedział, w którym f(x) rośnie to będzie (−2,−1> a maksymalny przedział, w którym f(x) maleje to będzie (1, 2> na Twoim rysunku z 17:36 też nie dołączmy, funkcja rośnie tylko w przedziale (−1, 1>

iteRacj@: 17:36 nie możemy dołączyć (−1), bo f(−1)=1 a np. f(0)=0,8 więc −1<0 ale f(−1)> f(0) i funkcja w tym przedziale nie rośnie

D4n1s0: Dziękuję, będę sobie po prostu sprawdzał tym z 18:09.