
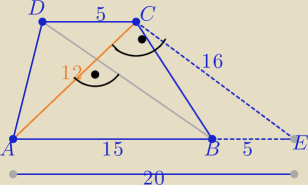
 1 sposób
ΔAEC jest prostokątny ..... bo 122+162=202
więc przekątne są prostopadłe
1 sposób
ΔAEC jest prostokątny ..... bo 122+162=202
więc przekątne są prostopadłe
| 1 | ||
P= | *12*16 =96 | |
| 2 |
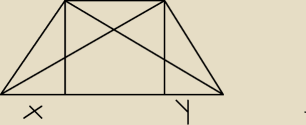 (5+y)2+h2=162
(5+x)2+h2=122
x+y=10
odejmując pierwsze rownanie od druiego
(5+y)2−(5+x)2=112
(y−x)(10+y+x)=112
(10−2x)*20=112−−−> x=11/5 −−−−−>(5+x)2+h2=122 −−−−> h=48/5
P=(5+15)/2 * 48/5 = 96
(5+y)2+h2=162
(5+x)2+h2=122
x+y=10
odejmując pierwsze rownanie od druiego
(5+y)2−(5+x)2=112
(y−x)(10+y+x)=112
(10−2x)*20=112−−−> x=11/5 −−−−−>(5+x)2+h2=122 −−−−> h=48/5
P=(5+15)/2 * 48/5 = 96
 Czy masz może inny pomysł na zadanie:
https://matematykaszkolna.pl/forum/376775.html
Czy masz może inny pomysł na zadanie:
https://matematykaszkolna.pl/forum/376775.html
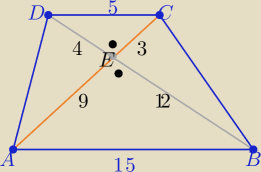 3 sposób
3 sposób
| 15 | ||
Z podobieństwa trójkątów ABE i DEC w skali k= | =3 | |
| 5 |
| 1 | ||
zatem P= | *12*16 = 96 | |
| 2 |