dowód z planimetrii rrrrrrr: Wykazać, że miejsce przecięcia się wysokości trójkąta ostrokątn. jest środkiem okręgu wpisanego w trójką spodkowy

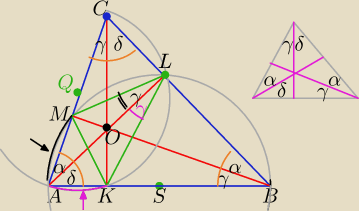
Mila: Z. O− ortocentrum ostrokątnego ΔABC T. punkt O jest środkiem okręgu wpisanego w ΔKLM Dowód: Środek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych kątów trójkąta. Należy wykazać, że półproste : KO, LO, MO są dwusiecznymi kątów ΔKLM 1)środek okręgu opisanego na ΔABLM leży w środku S przeciwprostokątnej ΔAMB, (okrąg ten jest jednocześnie opisany na ΔALB i AMC). ∡MLA=∡ABM=γ− kąty wpisane w okrąg o środku S oparte na tym samym łuku AM 2) środek okręgu opisanego na ΔAKLC leży w środku Q przeciwprostokątnej ΔALC, (okrąg ten jest jednocześnie opisany na ΔAKC i ΔALC). ∡ALK=∡ACK=γ− kąty wpisane w okrąg o środku Q oparte na tym samym łuku AM⇔ Półprosta LO jest dwusieczną kąta MLK =============================== 3) Analogicznie dla pozostałych kątów⇔ 4)Ortocentrum ΔABC jest punktem przecięcia dwusiecznych ΔKLM zatem jest środkiem okręgu wpisanego w ten trójkąt. cnw

Eta: Bardzo ładny dowód Mila Miałam podobny sposób ( półokręgi opisane na czworokątach) co na to samo wychodzi i dlatego już nie pisałam

Mila: Dziękuję bardzo za odpowiedź. Szkoda, że uczeń nie zainteresował się.

Eta: