Sprawdzenie zadań z rachunku prawdopodobieństwa Ania: 1. Wśród 70 pracowników pewnej firmy 45 ma wykształcenie wyższe, a 23 co najmniej 10 letnie doświadczenie . Ponadto 17 nie ma ani wykształcenia wyższego, ani 10 letniego doświadczenia. Znaleźć prawdopodobieństwo , że losowo wybrany pracownik ma 10 letnie doświadczenie, jeśli wiadomo że nie ma on wykształcenia wyższego . A = 45 A'=25 B=23 B'=47 A'nB' = 17 Mam policzyć A'nB? Jaki zastosować wzór? 2. Wiadomo z doświadczenia, że w pewnej gałęzi przemysłu spory między pracownikami a pracodawcami dotyczą 60% zarobków, w 15% warunków pracy, a w 25% innych spraw.Ponadto 45% sporów o zarobki jest rozwiązywanych bez strajku, 70% sporów o warunki pracy jest rozwiązywanych bez strajku i 40% sporów o inne sprawy jest rozwiązywanych bez strajku. Jakie jest prawdopodobieństwo, że spór między pracownikami, a pracodawcami w tej gałęzi przemysłu będzie rozwiązany bez strajku? 0,6*0,45+0,15*0,7+0,25*0,4 = 0,21+0,105+0,175=0,55 55% sporów bez strajku? Dziękuję z góry za pomoc

Pytający: 1. Rozróżniaj te dwa zapisy: A − jakiś tam zbiór |A| − moc/liczność powyższego zbioru Masz obliczyć "prawdopodobieństwo , że losowo wybrany pracownik ma 10 letnie doświadczenie, jeśli wiadomo że nie ma on wykształcenia wyższego". Znaczy się P(B|A') według Twoich oznaczeń (jeśli się dobrze domyślam − nie zapisałaś ich). Jest to prawdopodobieństwo warunkowe. Podpowiedź: |A'|=|A'∩B|+|A'∩B'| Chcesz sprawdzenia, to napisz wszystkie oznaczenia i obliczenia, nie skrawek. 2. Sposób dobry (0,6*0,45+0,15*0,7+0,25*0,4), ale są błędy rachunkowe.

Ania: Czyli w pierwszym będzie 25−17=8 czyli 8/70? W drugim faktycznie jest błąd, będzie 0,475 czyli 47,5% Czyli drugie zadanie dobrze było ok, gdyby nie błąd rachunkowy

Pytający: Drugie dobrze, pierwsze źle. Poczytaj: 1020.

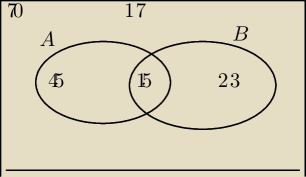
Ania: Zrobiłam coś takiego Zbiór A to osoby z wyższym wykształceniem Zbiór B to osoby z 10 letnim doświadczeniem Dodając to wszystko ( 45+23+17) otrzymałam wynik 85, a wiedząc, że pracowników jest tylko 70 to 85−70=15 i tak uzyskałam AnB. następnie odjęłam 23−15, żeby uzyskać B\A i wychodzi 8. Coś jeszcze muszę zrobić, bo uważam to za finalny wynik?

Pytający: P(B|A')=?

Ania: A' = 25 B = 23 P(AnB) = 8 P(B|A')= P(AnB)/A' = 8/23?

Ania: A' = 25 B = 23 P(AnB) = 15 P(B|A')= P(AnB)/A' = 15/23?* Sorki, tak?

Pytający: Nie tak. |A'|=|Ω|−|A|=70−45=25 |A'∩B|=|A'|−|A'∩B'|=25−17=8

	P(A'∩B)		|A'∩B|   |Ω|		|A'∩B|		8
P(B|A')=		=		=		=
	P(A')		|A'|   |Ω|		|A'|		25