Oblicz pole (całki)
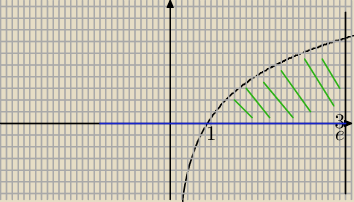
Aga: Oblicz pole obszaru ograniczonymi krzywymi: y=lnx, y=0, x=e3
Zadanie z działu całki.
5 cze 20:57
a7:
5 cze 21:00
Aga: a mogłabym prosić o obliczenia?
5 cze 21:06
5 cze 21:08
sushi:
a co robiłaś na zajęciach ?
5 cze 21:11
Aga: hehe nie ogarniałam

pomożesz?
5 cze 21:13
sushi:
⊂∫
5 cze 21:19
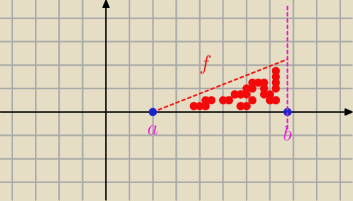
sushi:
∫ab f(x) dx
teraz patrz co jest u Ciebie i zapisz
5 cze 21:20
Aga: czyli ∫
lnx0 e
3 dx

5 cze 21:23
sushi:
jakie masz granice −−> na pierwotnym rysunku ?
5 cze 21:25
Aga: nie mam do tego rysunku
5 cze 21:25
sushi:
a7 zrobił rysunek
5 cze 21:31
Aga: 1 i 3 czyli ma być ∫
13 e
3 dx

5 cze 21:38
sushi:
e3 granica górna
5 cze 21:39
a7: a może
∫e3 1 lnx dx
5 cze 21:42
Aga: a no tak ∫e31 lnx dx ?
i coś jeszcze z tym trzeba zrobić?
5 cze 21:42
a7: no trzeba podstawić (tak jak się liczy całkę oznaczoną) i policzyć to pole
5 cze 21:44
5 cze 21:57
Jerzy:
P = 1∫e3lnxdx
Całkę liczysz przez części.
5 cze 21:58
5 cze 22:01
a7: pamiętaj, że e3 to stała (e≈2,71)
lne3=3, bo logarytm naturalny ma w podstawie e wiec jest logee3=3
5 cze 22:03
a7: x(lnx−1) +c
x(lnx−1) |1 e3
=e3(lne3−1) −1 (ln1−1) =
2e3+1≈2*19,90 +1=40.8
o ile nie pomyliłam się w obliczeniach
5 cze 22:10

 pomożesz?
pomożesz?
 ⊂∫
⊂∫

