eqweq Adam: Kombinatoryka Na ile sposobów można rozmieścić k nierozróżnialnych kul w n ponumerowanych szufladach, przy założeniu, że w każdej szufladzie może znaleźć się co najwyżej jedna kula? Co to znaczy że kula jest nierozróżnialna? Bo jeśli byłaby rozróżnialna to wówczas skorzystałbym z wariacji bez powtórzeń

PW: Nie ma co gadać. Tamtego → 375983 nie zrozumiałeś i wstawiasz następne?

a7: kula jest nierozróżnialna w odróżnieniu od kuli kolorowej lub numerowanej , od kul różnej wiekości itd.

Adam: aaaaaaa ok czyli są nierozróżnialne to w zasadzie wystarczy policzyć n^k

Mila: np. piłeczki do ping−ponga na ogół są białe i nierozróżnialne ( identyczne). Niech k=10 ( liczba piłeczek) n=4− liczba szuflad ponumerowanych 1) Liczba wszystkich możliwych rozmieszczeń jest równa liczbie rozwiązań równania: x₁+x₂+x₃+x₄=10 w zbiorze liczb całkowitych nieujemnych, czyli

10+4−1 4−1		13 3		1
	=		=		*13*12*11=..
				6

2) liczba rozmieszczeń , takich , że w każdej szufladzie znajdzie się co najmniej jedna kula, jest równa:

10−1 4−1		9 3
	=

Patrz rysunek:

	9 3
Trzy przegrody między kulkami możesz postawić na		sposoby

Masz ilustrację do sytuacji, że w I szufladzie są 3kule, w drugiej 3 kule, w trzeciej 2 i czwartej 2. 3) wracamy do Twojego zadania a) n=k tyle kul ile szuflad, w każdej szufladzie jedna kula Liczba sposobów − 1 b) k<n

n k
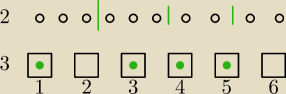
	− w każdej szufladzie jedna kula, lub szuflada pusta

( w każdej szufladzie co najwyżej jedna kula) n=6 − liczba szuflad k=4

6 4
	− wybór 4 szuflad z 6

na rysunku jedna sytuacja.