Zadania geometria 1 LO
Sandra: Witam! Jestem uczennicą 1 klasy liceum i mam problem z kilkoma zadaniami.
1. W trójkącie ABC poprowadzono dwusieczne kątów A i B. Przez punkt przecięcia się tych
dwusiecznych poprowadzono prostą l równoległą do boku AB. Prosta l przecina bok AC w punkcie
D, a bok BC w punkcie F. Udowodnij, że |DF|=|AD|+|BF|.
2. W trójkącie równoramiennym podstawa ma długość 30 cm. Środek ciężkości tego trójkąta
znajduje się w odległości 2 2/3 cm od podstawy. Oblicz obwód tego trójkąta.
3. W trójkącie równoramiennym ABC są dane= |AC|=|BC|=26 cm i |AB|=20 cm. Oblicz odległość
środka S wysokości CD od ramienia AC.
4. W trójkącie równoramiennym dane są długości podstawy a= 12 cm i wysokości h= 18cm. W trójkąt
ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po
jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion
trójkąta. Oblicz długości boków prostokąta.
5. Dane są długości boków a i b trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący
naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku b.
25 maj 18:07
Jerzy: za dużo na raz
25 maj 18:19
Mila:
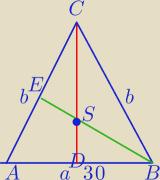
2)
W trójkącie równoramiennym podstawa ma długość 30 cm. Środek ciężkości tego trójkąta
znajduje się w odległości 2 2/3 cm od podstawy.
Oblicz obwód tego trójkąta.
Obw=2b+30
|AD|=15
2) oblicz b z tw. Pitagorasa ( ΔADC− Δprostokątny)
3) oblicz obwód Δ
25 maj 18:36
Sandra: To są zadania z mojego sprawdzianu, który miałam dzisiaj

Mila lubię Cię 😊 już mi kilka
razy pomogłaś. Studiujesz matematykę?
25 maj 19:45
Jerzy:
Nieładnie

. Piszę z telefonu,więc nick nie jest blue

25 maj 20:02
Mila:
A gdzie zadania Ety ?
25 maj 20:18
Jerzy:
Faktycznie dziwne.
25 maj 20:23
Mila:
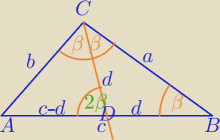
5. Dane są długości boków a i b trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący
naprzeciw tego boku jest
dwa razy większy od kąta leżącego naprzeciw boku b.
1)
CD
→− dwusieczna kąta C
|CD|=d
|AD|=c−d
Dalej albo z podobieństwa albo tw. sinusów i cosinusów, w zależności co już przerabiałaś.
Napisz .
25 maj 20:47
Sandra: Przerabiałam podobieństwo
25 maj 20:50
Mila:
Dobrze .
c.d
∡ADC=2β
ΔADC∼ΔABC⇔ patrzysz teraz, które boki leżą naprzeciw odpowiednich kątów i zapisujesz proporcje:
b
2=c*(c−d) i dc=ab
b
2=c
2−cd⇔b
2=c
2−ab
c
2=b
2+ab
c=
√b2+ab
c=
√b*(a+b)
==========
25 maj 21:53
Mila:
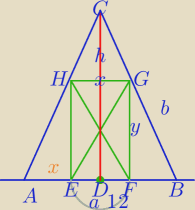
4. W trójkącie równoramiennym dane są długości podstawy a= 12 cm i wysokości h= 18cm.
W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie,
a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe
do ramion trójkąta.
Oblicz długości boków prostokąta.
1)
2) Z równoległości EG i AC⇒
x=4
y=12
x=4 i y=12
==========
25 maj 22:28
25 maj 22:33
Sandra: Mila ratujesz mi życie

jesteś the best!
26 maj 09:11
 2)
W trójkącie równoramiennym podstawa ma długość 30 cm. Środek ciężkości tego trójkąta
znajduje się w odległości 2 2/3 cm od podstawy.
Oblicz obwód tego trójkąta.
Obw=2b+30
2)
W trójkącie równoramiennym podstawa ma długość 30 cm. Środek ciężkości tego trójkąta
znajduje się w odległości 2 2/3 cm od podstawy.
Oblicz obwód tego trójkąta.
Obw=2b+30
 Mila lubię Cię 😊 już mi kilka
razy pomogłaś. Studiujesz matematykę?
Mila lubię Cię 😊 już mi kilka
razy pomogłaś. Studiujesz matematykę?
 . Piszę z telefonu,więc nick nie jest blue
. Piszę z telefonu,więc nick nie jest blue 
 5. Dane są długości boków a i b trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący
naprzeciw tego boku jest
dwa razy większy od kąta leżącego naprzeciw boku b.
1)
CD→− dwusieczna kąta C
|CD|=d
|AD|=c−d
Dalej albo z podobieństwa albo tw. sinusów i cosinusów, w zależności co już przerabiałaś.
Napisz .
5. Dane są długości boków a i b trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący
naprzeciw tego boku jest
dwa razy większy od kąta leżącego naprzeciw boku b.
1)
CD→− dwusieczna kąta C
|CD|=d
|AD|=c−d
Dalej albo z podobieństwa albo tw. sinusów i cosinusów, w zależności co już przerabiałaś.
Napisz .
 4. W trójkącie równoramiennym dane są długości podstawy a= 12 cm i wysokości h= 18cm.
W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie,
a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe
do ramion trójkąta.
Oblicz długości boków prostokąta.
1)
4. W trójkącie równoramiennym dane są długości podstawy a= 12 cm i wysokości h= 18cm.
W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie,
a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe
do ramion trójkąta.
Oblicz długości boków prostokąta.
1)
 jesteś the best!
jesteś the best!