... :)): W trójkącie równoramiennym ABC są dane : AC=BC=26cm , AB=20cm. Oblicz odległość środka S wysokości CD od ramienia AC

:)): ?

Eta: Rysuję

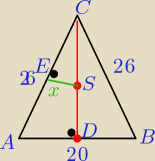
Eta: ICDI² = ICBI² − IDBI² więc ICDI²= 676 − 100 => ICDI = 24 to ICSI = 12 ΔSEC ~ Δ ADC więc:

IACI		ICSI
	=		.....podstaw i . policz x
IADI		x

:)): A ile ma AD

Eta: No przecież ,żze ¹₂ IABI bo to trójkąt ABC jest równoramienny czyli IADI = ¹₂ *20 => IADI = 10 ochhhhh

:)): No to mi i tak nie wychodzi taki wynik jak w ksiazce

:)): dobra juz mam dzieki

Eta: A jaki masz wynik w książce?

piotro: odległość jest pod kątem prostym, więc te trójkąty nie są podobne.

piotro: a nie, jednak są. sory

twerk: skąd wiadomo że ∡CES jest prosty?

Janek191: @twerk Bo odległość S od AC to długość najkrótszego odcinka czyli prostopadłego do AC.

Kamil: Skąd wiadomo że ΔADC ~ ΔSEC?

ite: Mają równe kąty. Spróbuj odpowiedzieć które i dlaczego.