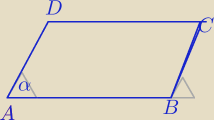
Trap Trap: Dany jest równoległobok ABCD, zbudowany na wektorach AB=−2a+3b i AD=10a+b. Oblicz długość wysokości DE równoległoboku, wiedząc, że |a|=4, |b|=2, kąt między a i b wynosi pi\3.

Adamm: https://matematykaszkolna.pl/forum/375382.html

Adamm: nie to, https://matematykaszkolna.pl/forum/375410.html

Adamm: Nie rozumiem po co dodawać te same zadania pod zmienionym nickiem, bo się czegoś nie rozumie. To forum jest na tyle wygodne, że można prowadzić pewną dyskusję, i jeśli czegoś nie rozumiesz, to zawsze możesz zapytać. No chyba że oczekujesz gotowych rozwiązań

Trap: Ja nie wiem jak mam policzyć wysokość, z jakiego wzoru? I dlaczego nie mogę policzyć pola z normalnego wzoru?

Adamm: P=a*h to wzór na pole równoległoboku, gdzie: a − długość boku, h − długość padającej na ten bok wysokości

	P
h=
	a

mamy pole, mamy długość boku, więc mamy długość wysokości możesz liczyć z "normalnego" wzoru, cokolwiek to znaczy kwestia tylko, co to znaczy że dany wzór jest normalny, a kiedy jest nienormalny pozostaje jeszcze kwestia etyczna, czy wzór można nazwać nienormalnym, bo przecież może się obrazić

Mila: |a|=4, |b|=2, P▱=|AB|*|AD|*sinα lub P_▱=|AB|*h |AB|*|AD|*sinα=|AB|*h h=|AD|*sinα

	π
1) |AB|2=(−2a+3b)2=4a2−12a o b+9b2==4*16−12*4*2 *cos		+9*4
	3

|AB|²=64+36−12*4=52

	π
|AD|2=(10a+b)2=100b2+20a o b+b2=100*16+20*4*2*cos		+4
	3

|AD|²=1604+80=1684 2) kąt między wektorami: AB^→ o AD^→=(−2a+3b) o (10a+b)=−20a²−2*a o b+30a o b+3*b²= =−20*16+28*4*2*cos(60^o)+3*4= =−320+112+12=−196 |AB|*|AD|*cosα=−196 2√13*2√421*cosα =−196

	49
cosα=−		− α− kąt rozwarty
	√13*√421

	3072
sin2α=
	13*421

	32√3
sinα=
	√13*421

	32√3
h=2√421*
	√13*421

	64√3
h=
	√13

==================== Jeśli obliczysz pole, to tak:

	32√3
P▱=2√13*2√421*		=32*4√3
	√13*421

32*4√3=2√13*h

	64√3
h=
	√13