22 maj 19:55
Mila:
Po kolacji popatrzę.
22 maj 19:55
miram : mila: Będę wdzięczna smacznego

22 maj 20:10
22 maj 20:13
Adamm:
mamy zbiór {(x, y)∊R2: y=f(x)}
przesuwamy go wzdłuż wektora v=[−2, 3]
to znaczy, że każdy punkt (x, y) przesuwamy o ten wektor
dostajemy zbiór {(x, y)+[−2, 3] : y=f(x)}={(x−2, y+3): y=f(x)}=
={(x, y): y−3=f(x+2)}
teraz staje się jasne dlaczego np. przy iksie odejmujemy pierwszą współrzędną wektora,
a do całej funkcji dodajemy drugą współrzędną
22 maj 20:19
Mila:
wykresy dobre, wzór xle napisałam.
Zaraz poprawię
22 maj 21:13
Mila:
| | 2 | |
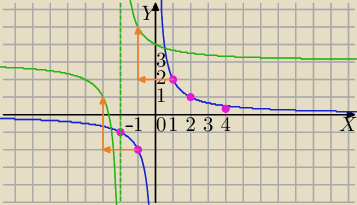
Wykres g(x) powstał z przesunięcia wykresu funkcji f(x)= |
| o wektor v=[−2,3] |
| | x | |
Po przesunięciu wykresu funkcji f(x) w wektor [a,b] otrzymamy wykres funkcji
g(x)=f(x−a)+b
Czyli
| | 2 | |
g(x)=f(x+2)+3⇔g(x)= |
| +3 |
| | x+2 | |
| | 2 | |
1) rysujesz wykres f(x)= |
| , x≠0 |
| | x | |
Punkty wykresu:
| | 1 | |
(1,2), (2,1),(4, |
| ,(−1,−2),(−2,−1) |
| | 2 | |
2) Przesuwasz wykres o 2 jednostki w lewo i 3 jednostki w górę
| | 2 | |
Otrzymujesz wykres g(x)= |
| +3 |
| | x+2 | |
x≠−2
22 maj 21:24

