optymalizacja
krzyss: Na kuli o promieniuR= 3 opisano stożek o możliwie najmniejszej objętości. Obliczwysokość oraz
promień podstawy tego stożka. Oblicz tę najmniejszą objętość.
15 maj 21:01
15 maj 21:16
Mila:
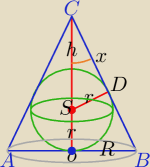
r=3
|OC|=h
|CS|=h−r, h>6
R
2*(h
2−6h+9)=9*(h
2+R
2)
R
2*h
2−6R
2*h+9R
2=9h
2+9R
2
R
2h
2−6R
2h=9h
2 /:h ⇔R
2*h−9h=6R
2
Licz pochodną.
15 maj 22:07
Eta: 
15 maj 22:21
Mila:
Nie mogłam znaleźć na forum, już kiedyś też rozwiązywałam na forum podobne zadanie.

15 maj 22:27
 r=3
r=3

