Prosze o wskazówki. Letty: Na kuli o promieniu R opisano stożek. Jaka musi być wysokość stożka aby miał on najmniejszą objętość?

Letty: Zaczęłam to liczyć z wzoru na promień okręgu wpisanego:

	2P		RH
r =		⇒ r =
	a+b+c		R + l

wiem że muszę utworzyć funkcje i szukać ekstremum, ale właśnie z tą funkcją mam problem.

	1
V=		πR2H
	3

ale nie wiem jak z tego pierwszego wzoru wyliczyć H żeby później wstawić do tej objętości.

piotrek:

Letty: pomoże ktoś?

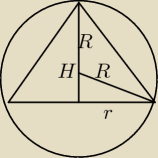
Beti: Może tak: (H − R)² + r² = R² h² − 2RH + R² + r² = R² r² = 2RH − H² V(H) = πr²H = πH(2RH − H²) = −πH³ + 2πRH² oraz D: 0 < H < 2R

Letty: Ale stożek jest opisany na kuli .

Letty: wie ktoś jak to zrobić?

Letty: ?

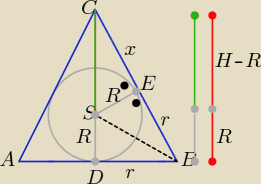
Eta: Z podobieństwa trójkątów DBC i SEC

H		x		H		x
	=		i		=
r		R		x+r		H−R

po przekształceniu otrzymasz:

	HR2
r2=		, założenie H >2R
	H−2R

	πH2R2
V(H) =
	3(H−2R)

dokończ...... V^'(H) =...... V^'(H)=0 ⇒ ............

Letty: dlaczego za r później podstawiłaś x + r ?