Trygonometria 123: Dla jakich wartości parametru istnieją rozwiązania równania: −sin²x−sinx+1−m=0 delta>0 tak wyznaczam górną granicę mój wynik: 5/4>m Jak wyznaczyć dolną? f(1)>0 f(−1)>0 ? co potem z tym zrobić

anka: https://matematykaszkolna.pl/forum/244144.html

Adamm: sposób w linku nie jest najlepszy

Adamm: sin²x+sinx=1−m wystarczy ustalić zbiór wartości f(x)=sin²x+sinx

123: A czy coś z tym f(1) i f(−1) nie da się zrobić?

PW: A co to jest według Ciebie f(1)?

123: Generalnie wartości w jakich mieście się sinus, jednak pytam bo w ten sposób znalazłem rozwiązania tego typu zadań: https://www.matematyka.pl/189757.htm

PW: Eeee...

Adamm: To jest błędny sposób

123: :(

123: A ten sposób z linku z jakiego względu jest zły? (poza czasochłonnością)

Adamm: Bo nie działa

123: Z tego pierwszego linku miałem na myśli

Adamm: Fakt, tam też był jakiś. Tamten nie jest zły, tylko czasochłonny

123: Jeszcze zapytam: f(x)=sin²x+sinx ZW to <−1/2, 1>? Dolna granica, z −b/2a=−1/2, a górna jest górną sinusa?

Adamm: podstawiasz pod sinusa zarówno −1 jak i 1 górna granica to 2

123: Ok, dziękuję Panu bardzo

Adamm: A dolna to nie jest wcale −1/2 (−1/2)²+(−1/2)=−1/4 − to jest dolna granica

123: Czyli bierzemy −1/2 z tego wzoru −b/2a i podstawiamy f(x)?

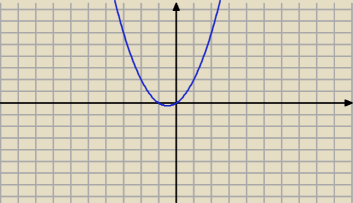
Adamm: f^*(t)=t²+t, −1≤t≤1 rozpatrywanie zbioru wartości f to to samo jakbyśmy rozpatrywali zbiór wartości f^* −b/(2a) to pierwsza współrzędna wierzchołka naszej paraboli wynosi −1/2, więc wierzchołek należy do tego wycinka paraboli dla t=−1/2 nasza parabola przyjmuje wartość najmniejszą (patrz rysunek) f^*(−1/2)=−1/4 − to jest nasza wartość najmniejsza największą mamy dla t=−1 lub t=1 f^*(1)=2, f^*(−1)=0, 2 jest większa, więc to jest maksimum

123: Ok, jeszcze raz bardzo Panu dziękuję

PW: Czasem ta miłość do Delty Naszej Kochanej okazuje się trudna. Popatrzmy jak łatwe jest rozwiązanie. Mamy zbadać istnienie rozwiązań równania (1) sin²x+sinx=1−m. Z oczywistych względów dla 1−m>2 równanie (1) nie ma rozwiązań (oba składniki lewej strony nie przekraczają 1). Dla (2) m<−1 nie ma rozwiązań.

	1
Po dodaniu do obu stron (1) liczby		dostajemy równanie równoważne
	4

	1		5
sin2x+sinx+		=		−m
	4		4

	1		5
(3) (sinx+		)2=		−m
	2		4

	5
Jest oczywiste, że równanie to nie ma rozwiązań dla		−m<0.
	4

Nie ma rozwiązań dla

	5
(4) m>		.
	4

Z (2) i (4) wynika, że badane równanie nie ma rozwiązań dla

	5
m∊(−∞,−1)∪(		,∞).
	4

Pozostaje zbadać, czy ma rozwiązania dla

	5
(5) −1≤m≤		.
	4

Dla krótkości zapisu oznaczmy

	5
(6)		−m = p2, , p>0.
	4

Równanie (3) można zapisać w postaci

	1
(sinx+		)2=p2
	2

	1		1
(sinx+		−p)(sinx+		+p)=0.
	2		2

Pierwszy czynnik przyjmuje wartość 0 gdy

	1
(7) sinx=p−		,
	2

aby istniało rozwiązanie musi być

	1		1
p−		≥−1 i p−		≤1
	2		2

p−0,5 i p≤1,5 Pierwsza nierówność jest spełniona w sposób oczywisty, druga − gdy

	5
		−m≤2,25
	4

m≥−1. Takie m należą do dziedziny (5), a więc rozwiązanie równania (7) istnieje.

	5
Odpowiedź. Równanie ma rozwiązania dla m∊[−1,		].
	4

PW: Korekta. W 6. wierszu od dołu powinno być p≥−0,5