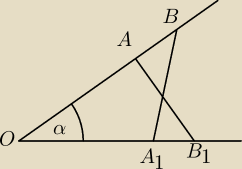
dwusieczna kiss: Dany jest kąt ostry α o wierzchołku O. Na jednym ramieniu tego kąta wybrano punkty A, B, a na drugim − punkty A1, B1 , w taki sposób, że IOAI=IOA1I i IOBI=IOB1I. Odcinki AB1 i A1B przecinają się w punkcie P. Wykaż, że punkt P należy do dwusiecznej kąta α

kiss: proszę o pomoc

Basia: trójkąty APB i A₁PB₁ są przystające (musisz to wykazać; potrafisz?) więc ich wysokości są równe a ich wysokości to odpowiednio odległość P od OA i od OA₁ czyli P jest równo odległy od ramion kąta α ⇔ P∊dwusiecznej kąta α

kiss: dziękuję bardzo! a jak właśnie wykazać przystawanie tych małych trójkątów (wiem ze ab i a1b1 beda takie same plus kąty wierzchołkowe ale co dalej )

Basia: AB=A₁B₁ bo A₁B₁ = OB₁−OA₁ = OB−OA = AB i cecha kbk

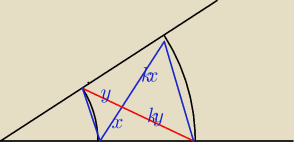
Basia: równoloeglość AA₁ i BB₁ z Talesa trapez jest równoramienny więc przekatne są równe x+kx = y+ky x(1+k) = y(1+k) x=y i kx=ky cecha bkb (nie kbk)

hubi: https://matematykaszkolna.pl/forum/374374.html

kiss: dziękuję!