Pole trapezu Pingwin4: W trapezie abcd ab II dc, przekątne przecinają się w punkcie e, ab=3dc a pole= 64. Oblicz pole.trójkąta aed

Pingwin4: Ktoś wie?

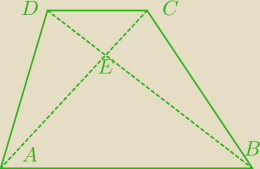
iteRacj@: |AB|=3|CD| ΔAEB≈ΔDCE dlaczego? P_ΔAEB=9P_ΔDCE P_ΔAEB+P_ΔDCE=64

iteRacj@: błąd w ostatnim równaniu , zaraz poprawiam

Pingwin4: Czemu to się równa 64

Pingwin4: Ach błąd

iteRacj@: P_ΔAEB+P_ΔDCE+P_ΔAED+P_ΔCEB=64 P_ΔAED=P_ΔCEB |DE|=3|EB| P_ΔACD=3P_ΔACB iteraz z tych zależności między polami wyliczysz P_ΔAED

iteRacj@: jeszcze jednan poprawka 3*P_ΔACD=P_ΔACB

iteRacj@: P_ΔAED=P_ΔCEB=12 P_ΔAEB=36 P_ΔCED=4

Pingwin4: Dlaczego de=3eb

iteRacj@: 3|DE|=|EB| pozamieniałam miejscami te odcinki

Pingwin4: Okej ale.skad wiemy ze to jest 3 razy wieksze

Pingwin4: A ze skali

Pingwin4: A skad wiemy ze =12

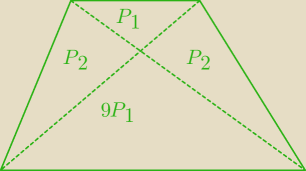
iteRacj@: 3*P_ΔACD=P_ΔACB P_ΔACD+P_ΔACB=64 P_ΔACD+3*P_ΔACD=64 P_ΔACD=16 P_ΔACD=P₁+P₂=16 P_ΔACB=9P₁+P₂=48 z tego P₁=4 a P₂=12

Eta:

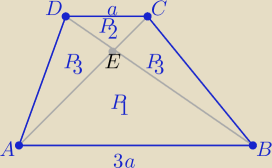
	3a
Z podobieństwa trójkątów ABE i CDE w skali k =		=3
	a

P(trapezu)= (k+1)²*P₂ i P₃=k*P₂

	64
to P2=		⇒ P2=4
	42

P₃=k*P₂ ⇒ P₃=12 P(AED)=12 =========

Eta: https://matematykaszkolna.pl/forum/191513.html tu masz wyprowadzenie tych wzorów

iteRacj@: i wcale nie trzeba było liczyć aż tylu pól

Eta: