 Witam. Mam problem z zadaniem ze stereometrii.
Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym alfa w którym ramię i krótsza
podstawa ma długośc a. Każda krawędź boczna ostrosłupa tworzy z płaszczyzną podstawy kąt Beta.
Oblicz objętość tego ostrosłupa.
Mianowicie wiem jak obliczyc pole podstawy w tym zadaniu. I wiem ze bedzie dalo sie tutaj
opisac okrąg. To pozwoli mi obliczyć R lecz nie wiem co dalej. W tresci widze ze Beta to kąt z
podstawą czy jak dobrze myśle to na rysunku Beta będzie miedzy krawędzią a przekątną trapezu.
I teraz w jaki sposób to Beta przenieś na wysokośc ostrosłupa jeśli nie jest powiedziane że
wysokośc pada na którąś z przekątnych? W sensie nie bedzie związku z tym Beta. Mam nadzieje,
że ktoś zrozumie o co mi chodzi i czego nie rozumiem
Witam. Mam problem z zadaniem ze stereometrii.
Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym alfa w którym ramię i krótsza
podstawa ma długośc a. Każda krawędź boczna ostrosłupa tworzy z płaszczyzną podstawy kąt Beta.
Oblicz objętość tego ostrosłupa.
Mianowicie wiem jak obliczyc pole podstawy w tym zadaniu. I wiem ze bedzie dalo sie tutaj
opisac okrąg. To pozwoli mi obliczyć R lecz nie wiem co dalej. W tresci widze ze Beta to kąt z
podstawą czy jak dobrze myśle to na rysunku Beta będzie miedzy krawędzią a przekątną trapezu.
I teraz w jaki sposób to Beta przenieś na wysokośc ostrosłupa jeśli nie jest powiedziane że
wysokośc pada na którąś z przekątnych? W sensie nie bedzie związku z tym Beta. Mam nadzieje,
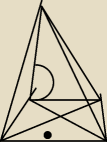
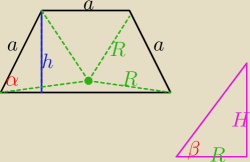
że ktoś zrozumie o co mi chodzi i czego nie rozumiem  Nie za bardzo umiem sie poslugiwac rysunkiem tutaj ale tam gdzie zaznaczylem kąt to bedzie Beta
a ta kropka to moze byc srodek okregu jak uzaleznic teraz beta od tego by wyliczyc wysokosc
ostroslupa
Nie za bardzo umiem sie poslugiwac rysunkiem tutaj ale tam gdzie zaznaczylem kąt to bedzie Beta
a ta kropka to moze byc srodek okregu jak uzaleznic teraz beta od tego by wyliczyc wysokosc
ostroslupa
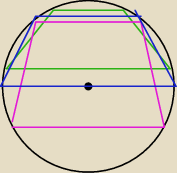 czemu nie .. tu masz kilka różnych podstaw..a spodek wysokości zawsze na czarnym
czemu nie .. tu masz kilka różnych podstaw..a spodek wysokości zawsze na czarnym
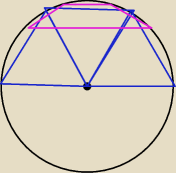 niebieski ma równe... z dokładnością do tutejszej rozdzielczości
różowy ma równe ..z dokładnością linijki na ekranie
niebieski ma równe... z dokładnością do tutejszej rozdzielczości
różowy ma równe ..z dokładnością linijki na ekranie 
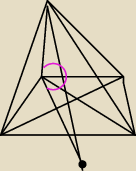 to juz nie wiem kogo sluchac
to juz nie wiem kogo sluchac  ale z rysunku tak jakby poprowadzic tą wysokosc do góry z
kropki to te kąty przy gornej podstawie nie wygladaja na takie same jak przy dolnej. Mowie o
katach miedzy krawdedzia a a plaszczyzna podstawy. Czyli na rysunku powinienem sobie oznaczac
to w jaki sposob jesli aniabb ma racje ? W taki jak przedstawilem będzie dobrze ? tutaj bedzie
Beta ? nw czy to jest plaszczyzna podstawy ? Czy do przekatnej powinienem poprowadzic, ale
wtedy jak bym ulozyl proporcje w tym trojkacie co narysowalem ? Moglby ktos to jasno
wytlumaczyc? Bylbym mega wdzieczny
ale z rysunku tak jakby poprowadzic tą wysokosc do góry z
kropki to te kąty przy gornej podstawie nie wygladaja na takie same jak przy dolnej. Mowie o
katach miedzy krawdedzia a a plaszczyzna podstawy. Czyli na rysunku powinienem sobie oznaczac
to w jaki sposob jesli aniabb ma racje ? W taki jak przedstawilem będzie dobrze ? tutaj bedzie
Beta ? nw czy to jest plaszczyzna podstawy ? Czy do przekatnej powinienem poprowadzic, ale
wtedy jak bym ulozyl proporcje w tym trojkacie co narysowalem ? Moglby ktos to jasno
wytlumaczyc? Bylbym mega wdzieczny  BO chce to zrozumiec
BO chce to zrozumiec 
| a3sin2α•tgβ | ||
V= | ||
| 3•tg(α/2)•2sin(α/2) |