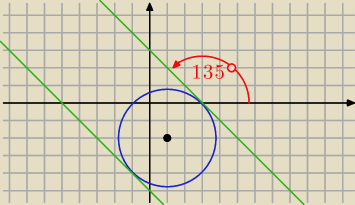
z QWERTY: Napisz równanie stycznej do okręgu x²+y²−2x+4y−3=0 i nachylonej do osi pod katem 135.

aniabb:

aniabb: y=−x−5 lub y=−x+3

QWERTY: A da się to zrobić bez rysunku

aniabb: wstawiasz do równania okręgu y=−x+b wyznaczasz deltę i delta =0 lub liczysz odległość środka okręgu od prostej y+x−b i ma być równa √8

QWERTY: czemu jest −x

aniabb: bo kąt jest 135° czyli a=tg (135°)= −1

aniabb: https://matematykaszkolna.pl/strona/1212.html

QWERTY: Sieczna x−y+1=0 przecina okrąg x²+y²−6x−2y+1=0 w punktach A i B. Przez punkty A i B poprowadzono styczne do okręgu, które się przecinają w punkcie C. Napisz równanie okręgu opisanego na trójkącie ABC o to mi chodzi Wiem że S=(3,1) A=(0,1) B=(3,4) C=(0,4) r=3 (x−3)²+(y−1)²=9

annabb: Podstaw A, B, C do równania okręgu i rozwiąż będzie a, b, r,

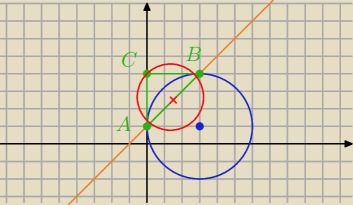
aniabb: trójkąt prostokątny więc środek w środku AB (x−3/2)²+(y−5/2)²=2,25