Przekątne trapezu równoramiennego ABCD qwe: Przekątne trapezu równoramiennego ABCD przecinają się w punkcie S . Przekątna AC tworzy z

	3
dłuższą podstawą AB kąt α i z ramieniem AD kąt β takie, że sin α =		i sin β
	5

	5
=		. Pole trapezu ABCD jest równe 448. Oblicz pole trójkąta ABD .
	13

aniabb: https://matematykaszkolna.pl/forum/371940.html

Mila:

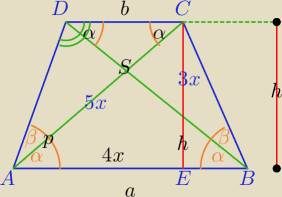
	3		5
sinα=		,sinβ=
	5		13

1) W ΔAEC: x− wspólna miara h=|CE|=3x, |AC|=p=5x, |AE|=4x

	a+b
|AE|=
	2

	448		4√21
PABCD=448=4x*3x⇔x2=		⇔x=
	12		3

	20√21
h=4√21 , p=
	3

======================= 2) W ΔACD: ∡D=180−(α+β)

p		b		20√21		5
	=		⇔b*sin(α+β)=		*
sin(180−(α+β))		sinβ		3		13

	3		5
sin(α+β)=sinα*cosβ+sinβ*cosα=		*cosβ+		*cosα
	5		13

	3		12		5		4		56
sin(α+β)=		*		+		*		=
	5		13		3		5		65

	56		100√21		125√21
b*		=		⇔b=
	65		39		42

3)

	1		125√21
PΔDCB=		*		*4√21=125
	2		42

4) P_ΔABD=448−125=323 =====================