trudne
Mat: W trapezie równoramiennym ABCD o polu 448
przekątne przecinają się w punkcie E i tworzą z dolną podstawą AB kąty α takie,że sinα=0,6
zaś z ramionami tworzą kąty β takie że sinβ= 5/13
Oblicz pole trójkąta ABD
18 mar 23:10
Basia: Masz wynik do tego zadania?
Niby to policzyłam, ale jakimś dziwnym sposobem i nie jestem pewna czy to ma sens.
19 mar 00:12
Eta:
Hej
Basia 
Mnie wyszło: P(ABD)=
323
A Tobie?
19 mar 00:30
Eta:
Może jeszcze
Mila poda wynik

19 mar 00:35
aniabb: mi wyszło Pole = 323
19 mar 00:35
Eta:

19 mar 00:35
19 mar 00:37
aniabb: część tego trójkąta to połowa trapezu więc 224 to murowane

a do tego jeszcze 99 ten mały
trójkącik obok

19 mar 00:38
Basia: ale mam błąd
19 mar 00:39
aniabb:

19 mar 00:40
Eta:
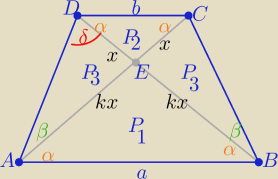
No to ja "swoimi" wzorkami

P
1=k
2*P
2 , P
3=k*P
2
| | P | |
i P(trapezu)=P=(k+1)2*P2 ⇒ (k+1)*P2*(k+1)=P ⇒ (k+1)*P2= |
| |
| | k+1 | |
P(ABD)= P
1+P
3 = k(k+1)*P
2
| | sinδ | |
Z tw. sinusów w ΔAED : k= |
| , δ=180o−(2α+β) |
| | sinβ | |
sinδ= sin2α*cosβ+cos2α*sinβ i po podstawieniu..........
| | 323 | | 13 | | 323 | |
k= |
| * |
| = |
| to k+1=.......... =448/25*13 |
| | 25*13 | | 5 | | 125 | |
P(ABD) = ....... =
323
19 mar 00:47
aniabb:
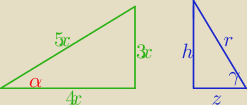
3x•4x/2=224 więc x=
√112/3 więc h=3x=
√336
γ=α+β więc sinγ=56/65 więc tgγ=56/33
w tym małym z=h/tgγ =
√336•33/56
19 mar 00:48
aniabb: wolę pitagorasa

19 mar 00:49
aniabb: Pole małego h•z/2 = 336•33/112 = 99
19 mar 00:50
Basia: inaczej zinterpretowałam treść zadania
α dałam tak jak Ty, ale β dałam tam gdzie Ty masz δ
musiało wyjść co innego

liczyłam podobnie

19 mar 00:51
Eta:
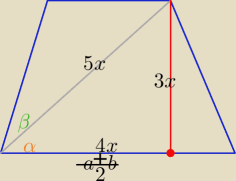
Można jeszcze tak ........ jak
aniaabb
19 mar 00:54
aniabb:
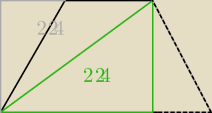
19 mar 00:55
aniabb: ale to tylko w równoramiennym tak działa

19 mar 00:55
Eta:
Tak, tak aniu
19 mar 00:56
aniabb: tak tylko rozpisuję czemu ta połówka taka pewna była

jakby ktoś kiedyś chciał się pouczyć

19 mar 00:57
Basia:
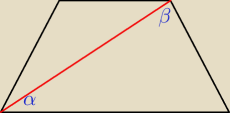
dalej tak jak
Eta albo tak jak
Ania, ale wyniki będą inne
taka interpretacja też chyba nie jest niepoprawna?
a zresztą czy ja wiem

19 mar 01:02
aniabb: upieram się przy minimum 224

poza tym α≈36° i β≈22° raczej nie dadzą ostrego na dole

w tym zestawieniu
19 mar 01:06
Eta:
Dobranoc
Dziewczyny 
19 mar 01:29
Basia: faktycznie nie dadzą ostrego
nie zwróciłam na to uwagi
tamten wynik jest do niczego w ogóle, coś tam zeżarłam
19 mar 01:34
Basia: 
19 mar 01:39
Basia:
| | 5 | |
z tego, że sinβ= |
| wcale nie wynika, że β≈22; to może być β≈158 |
| | 13 | |
tyle, że wtedy kąt przy C = α+β musiałby mieć więcej niż 180, a to jest niemożliwe
tak naprawdę to fakt, że to muszą być te kąty obok siebie wynika z tego, że
sin(α+β)>0 i cos(α+β)>0
czyli α+β jest kątem ostrym
19 mar 04:32
aniabb: jak widzę w funkcjach 3/5 i 5/13 albo 8/17 to widzę tam od razu trójkąty prostokątne

99%zadań bazuje na 3,4,5 5,12,13 8,15,17

chociaż ostatnio kilka trafiło mi się 7,24,25

i może z pięć razy 9,40,41

19 mar 09:35
 Mnie wyszło: P(ABD)=323
A Tobie?
Mnie wyszło: P(ABD)=323
A Tobie?



 a do tego jeszcze 99 ten mały
trójkącik obok
a do tego jeszcze 99 ten mały
trójkącik obok 

 No to ja "swoimi" wzorkami
No to ja "swoimi" wzorkami  P1=k2*P2 , P3=k*P2
P1=k2*P2 , P3=k*P2
 3x•4x/2=224 więc x=√112/3 więc h=3x=√336
γ=α+β więc sinγ=56/65 więc tgγ=56/33
w tym małym z=h/tgγ = √336•33/56
3x•4x/2=224 więc x=√112/3 więc h=3x=√336
γ=α+β więc sinγ=56/65 więc tgγ=56/33
w tym małym z=h/tgγ = √336•33/56

 liczyłam podobnie
liczyłam podobnie 
 Można jeszcze tak ........ jak aniaabb
Można jeszcze tak ........ jak aniaabb


 jakby ktoś kiedyś chciał się pouczyć
jakby ktoś kiedyś chciał się pouczyć 
 dalej tak jak Eta albo tak jak Ania, ale wyniki będą inne
taka interpretacja też chyba nie jest niepoprawna?
a zresztą czy ja wiem
dalej tak jak Eta albo tak jak Ania, ale wyniki będą inne
taka interpretacja też chyba nie jest niepoprawna?
a zresztą czy ja wiem 
 poza tym α≈36° i β≈22° raczej nie dadzą ostrego na dole
poza tym α≈36° i β≈22° raczej nie dadzą ostrego na dole  w tym zestawieniu
w tym zestawieniu


 99%zadań bazuje na 3,4,5 5,12,13 8,15,17
99%zadań bazuje na 3,4,5 5,12,13 8,15,17  chociaż ostatnio kilka trafiło mi się 7,24,25
chociaż ostatnio kilka trafiło mi się 7,24,25  i może z pięć razy 9,40,41
i może z pięć razy 9,40,41 