Planimetria, dwusieczna trójkąta prostokątnego Gustavo: W trójkącie prostokątnym ABC kąt przy wierzchołku A jest kąem prostym. Na przeciwprostokątnej CB zbudowano kwadrat CBDE o srodku symetrii w punkcie S (patrz rysunek). Wykaż, że odcinek AS zawiera się w dwusiecznej kąta CAB. Rysunek: https://prnt.sc/j2k5m5 Ogólnie miałem to zadanie na maturze próbnej dzisiaj, w ostatniej chwili naszło mnie oswiecenie, ale nie miałem czasu wykonać do końca, bo wybrałem zawiłą drogę (twierdzenie cosinusów i te o dwusiecznej). Jak to powinienem rozwiązać? Wydaje mi się, że zapomniałem o jakiejs własnosci, która by uczyniła te zadanie dużo łatwiejszym.

Gustavo: Tam gdzie zasłonięte jest litera "F", no i proszę nie zwracać uwagi na moje bazgroły na rysunku.

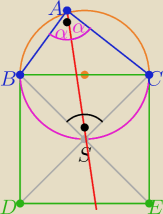
Eta: Na czworokącie ABSC można opisać okrąg ( dlaczego?..... łuki BS i SC są równej długości zatem kąty wpisane oparte na tych łukach są równe czyli odcinek As zawiera się w dwusiecznej kąta CAB

Gustavo: Aeh, własnie o okręgu myslałem, wyprowadziłem sobie nawet działania, ale myslałem, że to nie wystarczy to udowodnienia, że As zawiera się w dwusiecznej. (Przez takie kwiatki nienawidzę planimetrii) Czemu akurat łuki BS i SC? Nie wkradł się jakis błąd?

Eta: https://matematykaszkolna.pl/forum/40003.html