dwusieczna - dowód
Mira: Na przeciwprostokątnej AB trójkąta ABC na "zewnątrz" zbudowano kwadrat. Punkt K jest punktem
przecięcia przekątnych tego kwadratu. Udowonić,że półprosta CK jest dwusieczną kąta ACB.
26 lut 09:27
Mira: Pomóóóóóżcie!
26 lut 12:56
Eta:
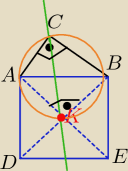
Przekątne kwadratu przecinają się pod kątem prostym
zatem I <AKBI= I<ACBI= 90
o
to na czworokącie AKBC można opisać okrąg , bo sumy kątów przeciwległych
tego czworokąta mają miary po 180
o
to kąt KCB i kąt KAC −− są kątami wpisanymi w ten okrąg i opartymi na łuku tej samej długości
miara łuków AK= BK
zatem miary kątów KCA = miara kąta KCB= 45
o
więc półprosta KC jest dwusieczną kąta ACB
c.b.d.o
26 lut 14:20
Eta:
Pomogłam , czekam na słowo ..... "dziękuję"

Tak dla przyzwoitości .
26 lut 14:37
Mira: Eta, wieeeeeeeelkie dzięki, ale na forum jest ktoś o nicku bardzo zbiżonym do mojego, może
wcześniej uzyskał od Ciebie pomoc bez podziękowania.
26 lut 14:57
Eta:

26 lut 15:56
 Przekątne kwadratu przecinają się pod kątem prostym
zatem I <AKBI= I<ACBI= 90o
to na czworokącie AKBC można opisać okrąg , bo sumy kątów przeciwległych
tego czworokąta mają miary po 180o
to kąt KCB i kąt KAC −− są kątami wpisanymi w ten okrąg i opartymi na łuku tej samej długości
miara łuków AK= BK
zatem miary kątów KCA = miara kąta KCB= 45o
więc półprosta KC jest dwusieczną kąta ACB
c.b.d.o
Przekątne kwadratu przecinają się pod kątem prostym
zatem I <AKBI= I<ACBI= 90o
to na czworokącie AKBC można opisać okrąg , bo sumy kątów przeciwległych
tego czworokąta mają miary po 180o
to kąt KCB i kąt KAC −− są kątami wpisanymi w ten okrąg i opartymi na łuku tej samej długości
miara łuków AK= BK
zatem miary kątów KCA = miara kąta KCB= 45o
więc półprosta KC jest dwusieczną kąta ACB
c.b.d.o
 Tak dla przyzwoitości .
Tak dla przyzwoitości .
