Eta where are you oleg: Nie ma Ety ani Mili kto mi pomoże ? https://matematykaszkolna.pl/forum/372400.html

Mila: Napisz jeszcze raz treść zadania, tam jest dużo komentarzy , jest nawet rozwiązanie.

oleg: Udowodnij że zbiorem wartości funkcji f(x)=log_0,5(x²−4x+20) jest zbiór (−∞,−4> najmniejszą wartość y=16 potem zrobilem f(16)= log_0,516= −4 problem mój polega na tym, że wydaje mi się, że zbiorem wartości funkcji f(x) jest właśnie odwrotnie <−4,∞) <−4,∞) nie mogę tego zrozumieć bo zbiór wartości funkcji g(x)= (x²−4x+20) jest dziedziną funkcji f(x) no i jak to się narysuje to ramiona w górę itd

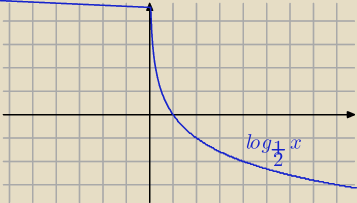
Blee: oleg ... zauważ, że podstawą logarytmu jest 0.5 czyli log_0.5 (x+1) > log_0.5 (x+2) innymi słowy − im większa wartośc logarytmowana tym mniejszą wartośc przyjmuje sama funkcja.

Blee: wyszło Ci, że g(x) = x²−4x + 20 przyjmuje minimum dla jakiejś tam wartości czyli wtedy właśnie f(x) = log_0.5 (g(x)) przyjmuje wartość NAJWIĘKSZĄ

Mila: 1) Dziedzina funkcji f(x): x²−4x+20>0 Parabola skierowana do góry, Δ=16−4*20<0 D_f=R 2) Zbiór wartości g(x)=x²−4x+20 x_w=2, g(2)=16− najmniejsza wartość g(x) Zw_g=<16,∞) 3) f(16)=log_0.5(16)=−4 największa wartość f(x) bo jest to funkcja malejąca , im większe argumenty [wartości g(x) ] tym mniejsze wartości f(x) log_0.5(2¹⁰)=−10 log_0.5( 2¹⁰⁰)=−100 Coś się wyjaśniło?

oleg: analizuje, .... normalnie jakas czarna dziura, ale dzieki

Eta: