do ety oleg: Do ETY mam do udowodnienia że zbiorem wartości funkcji f(x)=log_0,5(x²−4x+20) jest zbiór (−∞,−4> myślę tak, że zbiór wartości funkcji g(x)= (x²−4x+20) jest dziedziną funkcji f(x) wydaje mi się to logiczne Oczywiście g(x)=(x²−4x+20) to f.kwadratowa też logiczne która ma najmniejszą wartość y= 16 też logiczne czyli ZW g(x)=<16,∞) proste i logiczne jak budowa cepa no to dalej f(16)= log_0,516= −4 czyli finał i teraz mam jakaś ciemność bo wydaje mi się, że zbiorem wartości funkcji f(x) jest właśnie odwrotnie <−4,∞) nie mogę tego zrozumieć jakiś logiczny wykres może by przemówił, moze cos nie tak kombinuje niby wiem a jednak nie łapie. Proszę o pomoc ETE albo kogoś naprawde chcacego pomoc .

Maciess: Dziedziną funkcji f(x) nie będzie czasem x²−4x+20>0 Δ<0 a>0 czyli x∊R ?

Maciess: Chyba dobrze wyliczyłem ten wzorek

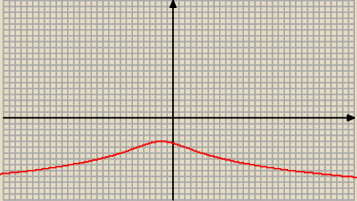
Pytający: Nie jestem Etą, ale możesz sobie policzyć f(32), czy f(64). Wartości maleją, bo podstawa logarytmu jest mniejsza od 1. Spójrz na drugi wykres: 219 i weź pod uwagę, że uwzględniasz jedynie część analogicznego wykresu na prawo od x=16.

Krysie60: Skoro prosisz Ete to po co potem jeszcze prosisz kogos innego skoro widzisz ze jest na forum ?

Maciess: f(x) = log _¹2 (x²−4x+20) g(x) = x²−4x+20 f(x) ma w podstawie liczbe z przedziału (0;1) czyli jest funkcją malejącą. g(x) jest określone dla wszystkich x−ów rzeczywistych. Wiemy jak wygląda jej wykres i możemy wskazać najmniejsza wartość (16) Nie wiem czy taki zapis jest poprawny ale zaryzykuje f(x)= log _¹2 (g(x)) Wiem, że wartości funkcji f(x) maleją gdy zwiększamy wartość argumentu. Czyli najmniejsza wartość g(x) będzie największą wartością f(x). Czyli jeśli wartość g(x) będzie rosła, to f(x) będzie maleć. Ja tak to rozumuje.

oleg: Krysie60: a ty skoro nie masz zamiaru pomoc to po co w ogóle piszesz i klepiesz bez sensu w kalwature. Czytaj ze zrozumieniem

oleg: Maciess: źle moze to napisalem bo wiem że dziedzina bedzie R tylko jja pisalem o ZW. nie wiem czy mnie zrozumiale4s?

Krysie60: Nie mam co robic dlatego klepie Zrozumienie jest moja mocna strona akuratnie Ucz sie dalej pilnie i nie marnuj czasu na dyskusje Zycze powodzenia na maturze .

oleg: Krysie60: nikt nie prosił takich jak ty o klepanie tylko o pomoc, ale jak widacnie rozumiesz tekstu pisanego wiec tez sie ucz tylko do matury to juz pewnie za pozno